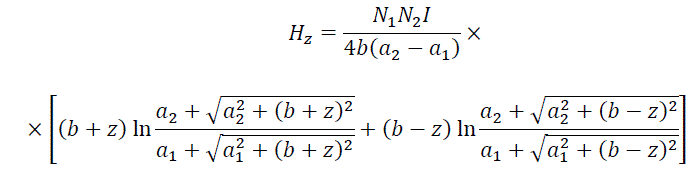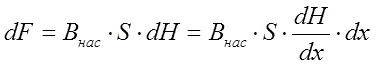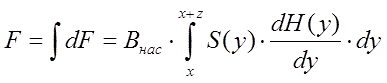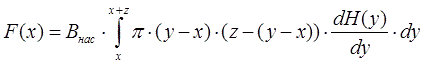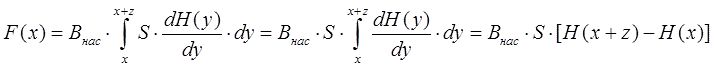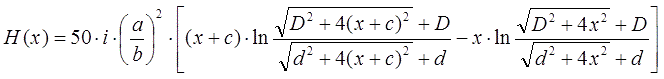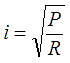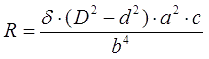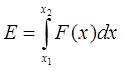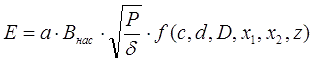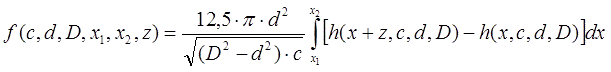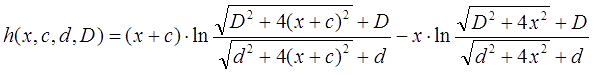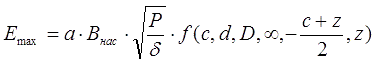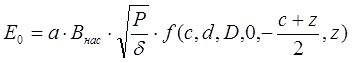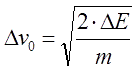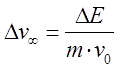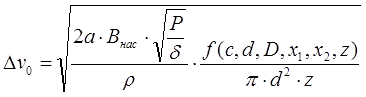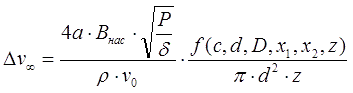| Главная » Статьи » Теоретические статьи » Математика coilgun |
В этой статье я обещал, что попробую более подробно проанализировать зависимости, которые выводятся из аналитических соотношений для полей и сил, действующих на ферромагнетик в электромагнитном ускорителе. Начнем с того, что перепишем этим соотношения. Здесь установлено, что действующая на цилиндрический снаряд длиной l и площадью сечения S сила, втягивающая его магнитное поле, имеющее зависимость от координаты H(x), может быть выражена так:
где Bнас - индукция насыщения материала снаряда. В другой публикации показано, что магнитное поле на оси многослойного соленоида длиной 2b, состоящего из N1 слоев по N2 витков в каждом слое, и имеющего внутренний радиус a1 и внешний радиус a2, для точки с координатой z от его центра имеет вид:
Там же я продемонстрировал, что поле весьма мало меняется при отклонении от оси катушки, и для расчетов по формуле (1) можно с хорошей точностью использовать величину H, определенную в соответствии с (2). Этих соотношений оказывается достаточно для получения очень интересных выводов о свойствах электромагнитных ускорителей.
1. Сила втягивания для бесконечно тонкого снаряда и тела произвольной формы. Начнем с того, что попробуем получить формулу для силы втягивания в катушку для тела произвольной геометрической формы, а не только цилиндрического объекта (описанного соотношением (1)). Для этого сначала рассмотрим такую абстракцию, как "бесконечно тонкий" снаряд. Устремляя в (1) длину сердечника к нулю, мы получим элемент силы, действующий на такое "блиноподобное" тело в следующем виде:
где dH - дифференциал (приращение) магнитного поля при смещении координаты на dx. Эта формула нам еще пригодится в дальнейшем - с помощью нее мы получим очень важную оценку для предельно достижимой в койлгане скорости наряда.
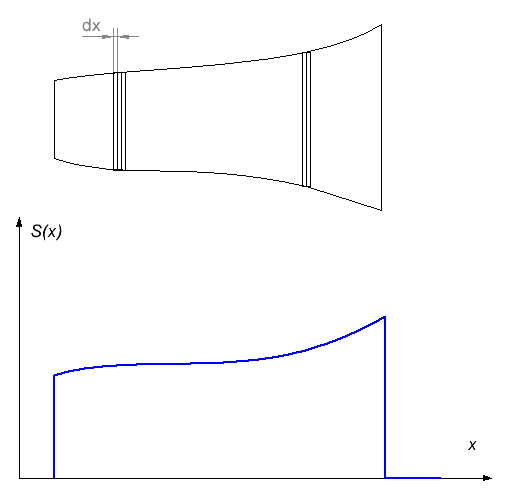
Дальше все довольно просто - любое тело можно представить как совокупность бесконечно тонких сечений, форма (площадь) которых изменяется про мере движения вдоль тела (см. рис. 1). Через x удобнее обозначить координату ближайшей к катушке точки (т. е. носа снаряда). Тогда, заменяя в соотношении (2) обозначение координаты на y и интегрируя вдоль тела длиной z, имеющего произвольную форму сечение S(y), получим такую формулу:
С помощью этого соотношения можно оценивать силу втягивания для любых тел, причем особенно простое описание получается для тел вращения (что, собственно, наиболее актуально для метательных снарядов). Например, для сердечника в виде шара получается такое описание втягивающей силы:
А для цилиндрического тела c площадью основания S
т. е., как и следовало ожидать, мы снова получили формулу (1) .
2. Определение скорости и кинетической энергии, приобретаемой снарядом при втягивании в катушку. Перепишем формулу (2) в более удобном виде, поменяв обозначения. Координату снаряда x будем отсчитывать от торца катушки (ближайшего в притягиваемому телу), внутренний и внешний диаметры катушки обозначим как d и D соответственно, ее длину - как с. Введем также коэффициент a, равный отношению калибра провода "по меди" b к его диаметру в изоляции (обычно при намотке получается a ≈ 0,75...0,85). Тогда
Здесь поле измеряется в единицах А/см, величины D, d и с - в сантиметрах, b - в миллиметрах. Как было указано ранее, подобная запись не очень удобна, т.к. текущий через катушку ток i может принимать разные значения в зависимости калибра провода и приложенного напряжения, поэтому логичнее за параметр источника питания принять его мощность P. Тогда предельный ток через обмотку будет определяться известным выражением
где R - омическое сопротивление провода, которое для цилиндрической обмотки с параметрами, указанными выше, в свою очередь, равно
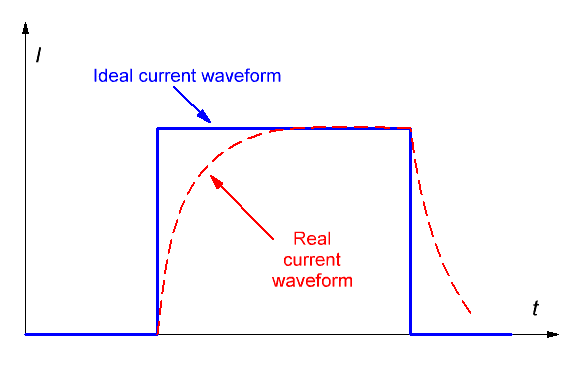
где δ - удельное сопротивление проводника обмотки (для меди δ ≈ 0,0175 Ом·мм2/м). Чтобы оценить кинетическую энергию и скорость, которую приобретает снаряд, нужно, вообще говоря, знать зависимость текущего в катушке тока от времени, которая определяется многими факторами - индуктивностью обмотки, свойствами источника питания (если речь идет о конденсаторе - его емкостью и внутренним сопротивлением), параметрами используемого для коммутации ключа и электрической цепи, которая применяется для гашения э.д.с. самоиндукции при прерывании тока. Кроме того, сам движущийся ферромагнитный снаряд наводит в катушке индуктивную э.д.с., которая может прибавляться или вычитаться из напряжения питания контура. Чтобы не рассматривать эти факторы, которые носят индивидуальный характер для каждого койлгана, сделаем ряд упрощающих предположений. Во-первых, пренебрежем влиянием сердечника на форму тока. Как показывает практика, это тем более верно, чем меньше скорость снаряда и чем больше напряженность поля (т. е. энергия, "вкачиваемая" в катушку при выстреле). Во-вторых, будем считать, что ток в катушке после включения мгновенно достигает максимального значения, определяемого ф-лой (6), а сразу после отключения спадает до нуля (т. е. импульс тока имеет прямоугольную форму во времени, см. рис. 2а). Такая ситуация является абстракцией, поскольку в реальной катушке индуктивность не дает току мгновенно изменяться. В результате катушку приходится "активировать" с некоторым запасом во времени - еще до того момента, когда снаряд достигает той области пространства, где действует заметная втягивающая сила. Из-за этого часть энергии тратится почти бесполезно - ток через катушку уже течет и греет собой провода, а снаряд еще толком не притягивается. Отключение тоже приходится производить заранее - наилучшим моментом для него была бы точка (так называемая "нулевая точка", НТ) , когда геометрический центр снаряда совпадает с серединой обмотки - здесь втягивающая сила начинает меняет знак и начинает тормозить снаряд (см. рис. 2б). Но из-за инерционности процессов приходится запирать управляющий ключ с некоторым запасом, иначе "хвост" тока на рис. 2а приводит к торможению снаряда (или же, если речь идет о системе с незапираемым ключом, приходится проектировать ее таким образом, чтобы ток в НТ уже был совсем небольшим).
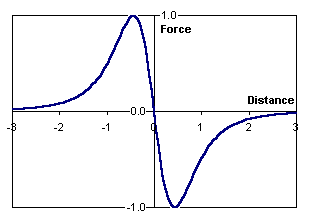
Рис. 2. Идеализованная (—) и реальная (-------) формы тока в катушке койлгана (а), и профиль втягивающей силы, действующей на снаряд (б).
В любом случае оказывается, что в реальной системе не удается использовалась всю область пространства (она на рисунке 2б расположена в левой полуплоскости), где происходит эффективное ускорение тела. В нашем же приближении это оказывается возможным, т. к. мы способны мгновенно включать и обесточивать катушку в оптимальный момент времени. Получается, что мы будем иметь наиболее благоприятные (оптимистичные) оценки для энергии и скорости снаряда, что, собственно, нам и нужно. Закончить эти рассуждения можно тем, наш абстрактный случай приблизительно описывает ситуацию в RLC-контуре с питающим конденсатором очень большого напряжения и емкости - тогда фронт нарастания тока будет очень крутым, а спад по достижении насыщения - очень пологим. Коммутироваться же такой контур должен ключом с бесконечным допустимым напряжением - тогда он сможет мгновенно прервать ток. То есть речь идет о неком "идеальном койлгане". Как известно из курса физики, приращение кинетической энергии можно вычислить через профиль действующей на тело силы F(x), проинтегрировав его по траектории ускорения между начальной и конечной точками x1 и x2:
Если считать, что ускоряемое тело имеет цилиндрическую форму с площадью основания S ≈ πd2/4 (т. е. стенки ствола очень тонкие и калибр снаряда равен внутреннем диаметру катушки), то подставляя в (8) соотношения (4), (5) - (7), получим:
где "геометрическая" функция
а через h обозначен форм-фактор катушки, стоящий в формуле (5) в квадратных скобках:
Как видно, максимальная приобретаемая кинетическая энергия пропорциональна индукции насыщения ускоряемого ферромагнетика, коэффициенту плотности намотки, а также корню квадратному из отношения электрической мощности и удельного сопротивления провода, которым намотана катушка (при этом она не зависит от диаметра этого провода). Функция f заключает в себе все геометрические свойства системы, в том числе начальную и конечную точку ускорения x1 и x2. С конечной точкой все однозначно - как показано выше, она должна совпадать с НТ, которая, как нетрудно показать для цилиндрических катушки длиной c и снаряда длиной z, дается выражением x2 = - ½(c+z). Что же касается начальной точки, то здесь могут быть различные подходы. Очевидно, чтобы оценить предельную энергию Emax, которую может получит снаряд, его разгон следует начинать с бесконечного удаления от катушки (x1 = ∞). В этом случае, однако, ускорение будет длиться неограниченно долго, и его КПД будет равен нулю (т. к. мощность потерь у нас постоянна и равна P). В реальных койлганах обычно катушка активируется в тот момент, когда снаряд заходит в нее своим носом, или где-то вблизи этой точки (x1 = 0). Возьмем этот случай как более близкий к практике (E0), и будем рассматривать наряду с предыдущим для иллюстрации. Тогда, с учетом (9):
Определив получаемую снарядом кинетическую энергию, можно оценить и развиваемую им скорость, точнее ее приращение Δv на рассматриваемой катушке. Рассмотрим два крайних случая относительно начальной (до включения тока) скорости снаряда v0: ускорения снаряда из состояния покоя или очень медленного движения (v0<<Δv), и с высокой начальной скоростью (v0>>Δv). Обозначим соответствующие приращения скорости как Δv0 и Δv∞. Первый случай, очевидно, соответствует стартовой ступени ускорителя, второй - катушке, расположенной где-то ближе к концу ствола многоступенчатого койлгана. Вспоминая известную "школьную" формулу для кинетической энергии E = ½mv2 и помня, что v=v0+Δv, имеем для энергии, полученной снарядом от данной ступени: ΔE = ½m (v2-v02)= ½m (v-v0)(v+v0)=½mΔv(2v0+Δv), откуда
Массу ускоряемого цилиндра длиной z и плотностью ρ легко выразить через его размеры: m = z·ρ·πd2/4. Тогда из соотношения (9) следует, что:
Из формул (14) следует, что приращение скорости, придаваемое снаряду при ускорении из состояния покоя, пропорционально корню четвертой степени из мощности тока, а при большой начальной скорости - квадратному корню из P. Интересно, что на страничке соотношений для электромагнитных ускорителей я из более простых соображений получил, что в целом для койлгана, работающего в режиме постоянного тока и равноускоренного движения снаряда, выходная скорость пропорциональна кубическому корню из P, что хорошо соответствует "золотой середине" между двумя крайними случаями, рассмотренными выше. Используя соотношения (12), можно также получить выражения для приращения скорости снаряда, ускоряемого с бесконечного удаления от катушки (x1 = ∞, это будет предельно достижимая в койлгане данной конфигурации скорость), и от конкретной точки x1. Оценки, сделанные по ф-лам (12) и (13), должны обладать довольно хорошей точностью (настолько, насколько справедливы соотношения (1) и (2) в начале этой статьи). Казалось бы, зная выражения для скорости и энергии снаряда, легко оценить и другой ключевой параметр койлгана - его КПД. Однако, оказывается, что это не так. Дело в том, что для этого необходимо знать энергию Eext = P·t0, затраченную из внешнего источника за время разгона снаряда t0, а это сделать трудновато, причем в разных случаях по различным причинам. При нулевой начальной скорости нам будет неизвестно t0, т. к. закон движения снаряда x(t) определяется не только постоянной величиной действующей в цепи мощности P, но и профилем действующей силы (10). В итоге для оценки t0 в каждом случае необходимо проведение численного моделирования - простым аналитическим способом его не выразить. Для высокой начальной скорости v0 вроде бы можно принять время движения через катушку (длиной с) за постоянную величину t0 ≈ с/v0 и получить КПД в виде некоторой величины, пропорциональной v0 , как это сделано здесь. В результате можно сделать абсурдный вывод, что КПД койлгана при увеличении скорости снаряда будет стремиться к бесконечности.... Причина этого заблуждения проста - при выводе соотношений (1), (5) и (9) мы пренебрегали влиянием на магнитное поле катушки самого снаряда и считали рассеиваемую мощность в цепи постоянной, а это справедливо только при небольшой скорости тела и сильных (и постоянных) токах в обмотке. Но при высокой величине v0 ток катушки (при постоянном количестве витков) не будет успевать нарастать до значений, близких к (6) из-за влияния индуктивности - именно поэтому в многоступенчатых системах катушки по мере роста номера ступени наматываются все более толстым проводом, или же содержат все меньше витков. Кроме того, как мы уже упоминали выше, стремительно движущийся снаряд производит в катушке индуктивную э.д.с., которая может оказывать существенное воздействие на форму тока в цепи. Этот эффект я в свое время даже использовал для построения оригинального индукционного датчика положения снаряда в стволе ускорителя. На рисунке ниже приведены осциллограммы тока, полученные при работе с этим датчиком - на них видны характерные колебания, вызываемые движением ферромагнетика внутри катушки. Рис. 3. Колебания тока катушки, вызванные индуктивной э.д.с. от движущегося внутри нее снаряда.
Таким образом, при росте начальной скорости наряда приближения постоянного тока и сильного поля утрачивают свою справедливость, и для определения КПД опять-таки необходимо использование численного моделирования.
| |||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 577 | | | |||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |