Как показано в предыдущей публикации, задача оптимизация параметров ускоряющей катушки в койлгане неразрывно связана с формой снаряда. Поэтому, в завершение этого короткого цикла статей, необходимо сказать несколько слов про ускоряемое тело, а точнее, его оптимальную форму, которая обеспечивает максимальную эффективность преобразования электрической энергии ΔE_electric в кинетическую ΔE_kinetic (что, собственно и является главной функцией койлгана). Для этого еще раз перепишем полученную нами формулу для воздействующей на снаряд силы:

F = Bнас ·S ·[H(x+ l) - H(x)]

(1)

где B_нас - индукция насыщения сердечника, H(x) и H(x+l) - напряженность поля, создаваемого катушкой в плоскости переднего торца снаряда (имеющего координату x) и на заднего его торце (с координатой x+l, т.е. сердечник имеет длину l), а S - площадь сечения снаряда в плоскости, перпендикулярной магнитному потоку.

Если считать, что электрическая мощность P в катушке постоянна (это довольно грубое приближение, т. к. вообще говоря нужно учитывать динамику изменения тока), то КПД ускорения η, очевидно, будет пропорционален этой ускоряющей силе:

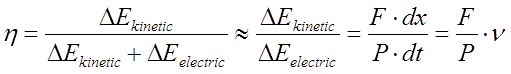(2)

Кроме того, видно, что КПД растет с увеличением начальной скорости v сердечника.

Что нам дают этим соотношения?

Разберемся сначала с длиной снаряда.

Для этого заметим, что формуле (1) в скобках стоит разница напряженностей на передней и задней гранях снаряда. То есть наилучшей будет такая его длина, при которой "нос" снаряда  наиболее продолжительное время находится в области максимального поля, а его "хвост" - минимального. Тогда на снаряд будет действовать наибольшая ускоряющая сила. 

С этой точки зрения самым оптимальным будет бесконечно длинный снаряд - на его задней грани всегда H = 0 просто потому, что она бесконечно удалена от источника поля - катушки (см. рис. 1). 

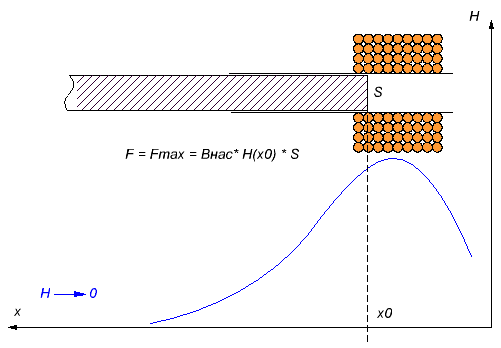Рис. 1. Максимальная ускоряющая сила действует на бесконечно длинный снаряд. Соответственно, он же будет приобретать максимальную кинетическую энергию  при прохождении катушки.

 

Проблема, однако, в том, что в соответствии с ф-лой (2), для получения ощутимого КПД ускорения, снаряд должен иметь какую-то скорость. Из школьного курса физики известно, что при получении каким-либо телом фиксированного количества кинетической энергии рост его скорости обратно пропорционален массе:

dE = d (mv2/2) = mv·dv, откуда dv = dE / (m·v)

(3)

Поэтому для разгона бесконечно длинного снаряда надо затратить (кто бы мог подумать !) неограниченное количество энергии... 

Если теперь перейти от математических абстракций к реальной жизни, то понятно, что увеличение длины снаряда выше определенного значения уже не приведет к повышению ускоряющей силы, поскольку поле на его заднем торце уже и так будет близко у нулю. В то же время, масса снаряда (при фиксированном калибре) растет просто пропорционально его длине. Поэтому, начиная с какого-то момента, увеличение длины метаемого тела начнет вызывать снижение КПД.

С другой стороны, совсем короткий (плоский) снаряд хоть и будет хорошо ускоряться, но из-за малой массы кинетическая энергия такого "блина" будет стремиться к нулю.

Таким образом, следует ожидать, что для каждого фиксированного набора параметров системы (размер катушки, энергия конденсаторов, начальная скорость снаряда) будет существовать некая оптимальная длина ускоряемого тела.

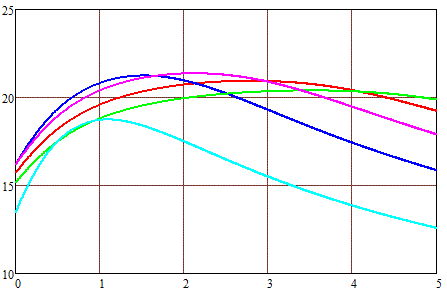
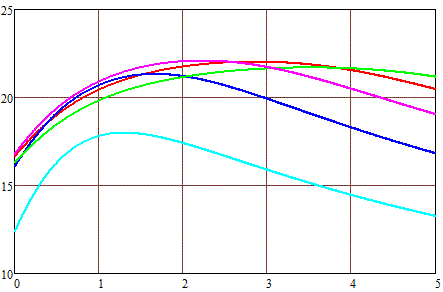
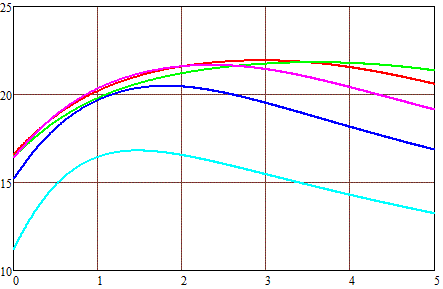
На рис. 2 приведены результаты расчетов максимальной скорости снарядов в зависимости от их длины, достижимых при разгоне электрическим током мощностью 10000 Вт в катушке внутренним диаметром 1 см и наружным 2 (а), 3 (б) и 4 (в) см. Для расчетов использовались формулы для пространственных зависимостей напряженности поля, приведенные в прошлой статье, и значение индукции насыщения железа В_нас = 2 Тл. Предполагалось, что в момент включения тока передний торец снаряда совпадает с передней плоскостью катушки, а в момент отключения снаряд полностью входит в катушку (точнее, геометрические центры катушки и снаряда совпадают - тогда втягивающая сила становится равной нулю). Разгон ведется из состояния покоя (т. е. от нулевой начальной скорости снаряда), при этом считалось, что возрастание и убывание тока в обмотке происходит мгновенно.

(а)	Рис. 2. Максимальная скорость снаряда калибром 1 см (по вертикальной оси) в зависимости от его длины (по горизонтальной оси). Наружный диаметр обмотки 2 см (а), 3 см(б) и 4 см (в).
(б)	Длина катушек: — - 1 см — - 2 см — - 3 см — - 4 см — - 5 см
(в)

 

Из этих зависимостей вытекают некоторые интересные следствия, но для их вывода потребуется работа с довольно сложными математическими формулами, поэтому я постараюсь проанализировать их позже в отдельной публикации. Пока же можно просто отметить, что для каждой длины катушки существует оптимальная длина снаряда, которая для коротких катушек чуть больше их длины, а для длинных - чуть меньше. При этом увеличение толщины обмотки приводит к смещению максимума скорости в сторону более протяженных снарядов, хотя само значение этого максимума меняется слабо. 

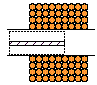
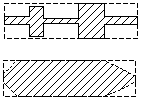
Теперь рассмотрим как будет влиять на ускорение снаряда его диаметр (при сохранении постоянного калибра ускоряющих катушек ). Для начала, представим, что мы вместо цилиндра, "подогнанного" под внутренний диаметр катушек, поместили внутрь койлгана тонкий стержень той же длины l (см. рис. 3 (а)). Как изменится его скорость?

Как показано здесь, вектор напряженности в пределах сечения снаряда меняется очень слабо, поэтому согласно формуле (1), ускоряющая сила будет пропорциональна просто площади торца снаряда S. С другой стороны, масса снаряда при сохранении его длины и материала (т. е. его плотности), тоже будет пропорциональна S. Поскольку, согласно второму закону Ньютона, ускорение тела прямо пропорционально силе и обратно пропорционально его массе (dv/dt = F/m), то получается, что "тонкий" снаряд будет ускоряться совершенно так же, как и "толстый". Иными словами, скорость снаряда не зависит от его диаметра. Но, поскольку кинетическая энергия снаряда пропорциональна его массе, то КПД ускорения "тонкого" стержня будет меньше, чем "толстого". 

(а)

(б)

Рис. 3. Тонкий стержень ускоряется так же, как цилиндр аналогичной длины (а). Различные формы тел, ускоряемые с меньшим КПД, чем простой цилиндр (б).

 

Легко сообразить, что это рассуждение распространяется и на более сложные формы метаемого тела - любые сердечники, имеющие какие-либо сужения и выемки (см. рис. 3 (б)), будут ускоряться с пониженным КПД относительно сплошного цилиндрического тела...

К такому же выводу можно прийти и на основании того простого рассуждения, что сердечник должен "собирать" в себя максимальное количество линий магнитного потока, на генерацию которого уходит вся запасенная в койлгане энергия. Поэтому он должен, по возможности, заполнять все доступное ему пространство внутри катушки, а любые отклонения от цилиндрической формы позволяют части поля бесполезно рассеяться.  

Кстати, отсюда же следует, что стенки "ствола" койлгана ( обычно это просто трубка, на которую снаружи наматываются катушки, а внутри движется снаряд) должны иметь минимальную толщину.

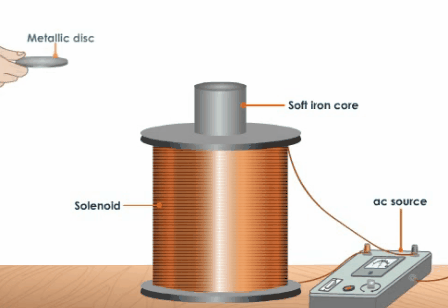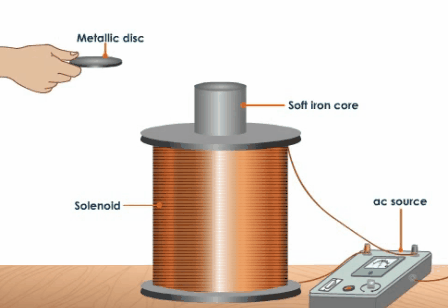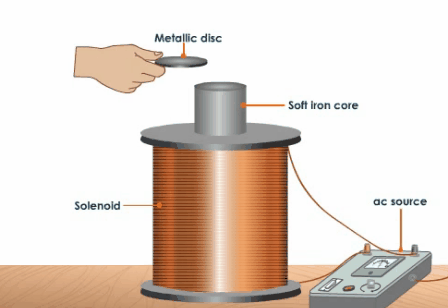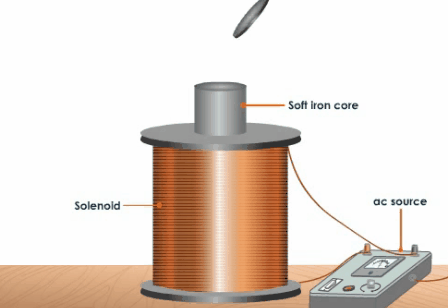
Еще одним интересным вопросом является влияние так называемых "вихревых токов" ("токов Фуко"), которые должны возникать в сплошном теле снаряда при воздействии на него переменного магнитного поля. Поскольку по правилу электромагнитной индукции эти токи будут направлены противоположно индуцирующим их токам во внешней обмотке, то результирующая сила будет выталкивать снаряд из катушки. На этом принципе работают индукционные ускорители ("Томсон-ган"), но в нашем случае этот эффект будет противодействовать ускорению (которое в койлгане происходит, наоборот,  за счет втягивания ферромагнетика магнитным полем). Помимо всего прочего, вихревые токи могут приводить к разогреву проводника (который иногда используется в промышленности для закалки поверхностных слоев массивных стальных деталей в специальных индукционных печах, см. рис. 4).

Рис. 4. Возникновение "токов Фуко" в массивном проводнике (слева) и их механическое и тепловое проявление (справа). 

 

Для подавления вихревых токов часто предлагается изготавливать снаряд для гауссовки в виде набора плоских изолированных слоев (по типу сердечников сетевых трансформаторов), либо делать в нем продольный пропил до центральной оси. Использование непроводящих материалов вроде феррита (по примеру магнитопроводов высокочастотных трансформаторов) в нашем случае не подходит, т. к. они обладают низким значением индукции насыщения B_нас. 

Однако, при работе с обычным любительским койлганом эффект "токов Фуко" заметить сложно - большинство экспериментаторов-любителей сходятся во мнении, что в койлганах они сколько-нибудь заметным образом себя не проявляют. Более серьезные эксперименты и попытки расчетов с использованием численного моделирования подтверждают этот факт. Так, в статье [2] проводится сравнительный эксперимент по стрельбе из многоступенчатого ускорителя сплошным снарядом и снарядом с продольным пазом. Последний действительно ускоряется немного лучше, но разница эта совсем невелика (повышение КПД составило с 2,23% до 2,40 %). Б.Слэйд по результатам расчета в своем оригинальном симуляторе установил [3], что влияние вихревых токов на скорость несущественно, но возрастает при введении в систему внешнего (неподвижного) магнитопровода. Правда, установка такого магнитопровода в сколько-нибудь мощных койлганах является не особенно целесообразной, как я показал в этих работах.

Что же касается тепловых потерь, то их расчету в сердечнике катушечного ускорителя посвящены публикация [1]. 

Многие новички выступают с идеей использования в качестве ускоряемого тела сильного постоянного магнита (например, неодимового). Такое желание, видимо, возникает на почве увлечения маломощными стрелялками на основе цепочки постоянных магнитов, великое множество которых можно найти в Интернете (кстати говоря, именно такие штуки изначально и назывались "пушками Гаусса").  

Рис. 5. "Классическая" пушка Гаусса на постоянных магнитах.

Действительно, ассортимент магнитов сейчас довольно велик, и их можно приобрести в удобном (для использования в качестве снарядов) виде стержней почти любого калибра и длины. Проблема здесь в том, что поля таких магнитов хоть и кажутся большими, но уступают полям, которые присутствуют даже в слабеньких катушечных ускорителях. Поэтому предварительно намагниченное ускоряемое тело будет иметь преимущество только в начальный момент разгона, когда ток в обмотках не достиг существенных значений - дальше любой ферромагнетик уходит в насыщение, и более важную роль начинает играть величина B_нас. А поскольку индукция насыщения у магнитно-жестких материалов, используемых в постоянных магнитах, обычно намного меньше, чем у простого железа, то и какая-либо выгода от применения их в койлганах отсутствует... 

Более логичным выглядит предложение использовать в качестве материала снаряда специальные сплавы с повышенным значением B_нас. Так, сплав пермендюр состоит из 30—50 % кобальта, 1,5—2 % ванадия и остальное — железо. Он обладает наивысшей из всех известных ферромагнетиков индукцией насыщения до 2,43 Тл. К сожалению, такой материал и ему подобные слишком дороги и "труднодоставаемы" для любительских экспериментов. Поскольку снаряды в них являются лишь расходным материалом, то целесообразность связанных с этим затрат внушает сомнение, притом что прогнозируемое повышение эффективности ускорителей в случае их применения не так уж велико.

 

В заключение стоит заметить, что помимо рассмотренных вопросов оптимизации ускорения снаряда внутри койлгана, существует еще отдельная проблематика поведения снаряда на том этапе, когда он уже покинул ствол ускорителя и движется в сторону цели во внешней среде (в оружейной теории этот раздел называется "внешняя баллистика"). Этой тематике применительно к гаусс-ганам уделяется очень мало внимания. Например, почти не исследуются вопросы стабилизации снаряда в полете. Единственным известным мне исключением является та же публикация [2], где отдельно изучалась влияние оперения на устойчивость траектории сердечника. Ваш покорный слуга также внес посильный вклад, опубликовав пару статей на этом сайте. 

Характерной особенностью койлганов в этой части является тот факт, что форма их снаряда сильно влияет на эффективность ускорения (чего нет, например, в огнестрельном или пневматическом оружии), поэтому здесь у экспериментаторов в определенном смысле "связаны руки". 

Еще одним не до конца проясненным моментом остается оптимизация формы носовой части метаемого тела. Снаряд ведь должен не только разогнаться до максимальной скорости и долететь до мишени, но и проникнуть в нее на максимальную глубину. При этом форма носа в виде плоской грани, оптимальная с точки зрения ускорения, очевидно, не придает снаряду хорошей поражающей способности. 

 

Выводы:

1) Оптимальная с точки зрения КПД длина ускоряемого тела должна подбираться под конкретный фиксированный набор параметров системы (размер катушки, энергия конденсаторов, начальная скорость снаряда). Приращение кинетической энергии ускоряемого тела тем выше, чем  больше его длина.

2) Ускорение тела не зависит от его диаметра. Поэтому для получения максимального КПД целесообразно использовать снаряды цилиндрической формы, максимально заполняющие внутренний объем катушки.

3) В качестве материала для снаряда лучше всего подходит обычное железо. Поскольку вихревые токи в койлганах заметно себя не проявляют, то принятие мер для борьбы с ними (например, изготовление метаемого тела в виде слоистой структуры) нецелесообразно, также как и использование каких-либо специальных дорогостоящих материалов с повышенной индукцией насыщения.

 

Литература.

[1]. H.Chen et al, "Iron Loss Analysis of Double-Sided Linear Switched Reluctance Launcher", IEEE Trans. on Plasma Science, May 2019, vol. 47 (5), p. 2323.

[2]. H.Xiang et al, "Design and Experiment of Reluctance Electromagnetic Launcher with New Style Armature", IEEE Trans. on Plasma Science, May 2013, vol. 41 (5), p. 1066.

[3]. http://users.skynet.be/BillsPage/SimulationResults1.0.pdf 

[4]. S.Kim and J.Kim, "Optimal design of a coil gun projectile by analyzing the drag coefficient and electromagnetic force on the projectile", Journal of Mechanical Science and Technology, vol. 34 (7), 2020, p. 2903.

 

< Назад