Расчет характеристик многоступенчатого койлгана, работающего по принципу "бегущего поля".

 

Данная работа была проделана по просьбе Dantist'a, занимающегося созданием ускорителя DD11. Этот интересный проект подробно описан в соответствующей  ветке форума "Оружие будущего". Особенностью DD11 является его функционирование в режиме "бегущего поля", то есть создание с помощью цепочки плоских близко расположенных катушек области градиента магнитного поля, движущегося по стволу ускорителя вместе со снарядом. Таким образом должно быть достигнуто постоянное нахождение ускоряемого тела в области максимальной воздействующей силы. Этим данная схема выгодно отличается от обычных конфигураций койлганов с длинными катушками, где снаряд периодически попадает в зоны ускоряющей и тормозящей сил (подробнее можно посмотреть например здесь). Кроме того, автор намерен реализовать подключение ступеней своего ускорителя по схеме "косого полумоста", которая за счет возврата части энергии в питающую емкость (рекуперации) имеет повышенный КПД (некоторые численные оценки приведены мной здесь).

На рис. 1. приведены геометрические характеристики системы, включая форму магнитопровода, снаряда и собственно ускоряющих катушек. Как видно, последние имеют плоскую "блиноподобную" форму, которая обладает повышенной эффективностью при рекуперации.

Рис. 1. Геометрические параметры койлгана DD11.

 

Однако при попытке математического моделирования этой конструкции  возникла проблема. 

Дело в том, что практически все существующие скрипты на основе FEMM, которые сейчас используются гауссостроителями, позволяют моделировать воздействие на снаряд только одной катушки одновременно. Но сама суть реализации алгоритма "бегущего поля" состоит в единовременной работе нескольких (конкретно для DD11 - трех) ступеней. Наличие снаряда сложной формы и магнитопровода вносит дополнительные затруднения.

В итоге довольно кропотливой работы мной был написан скрипт, позволяющий реализовать моделирование этой системы. За основу был взят старый скрипт для многоступенчатой тиристорной системы с сайта Петровича и полностью переработан (проведена адаптация программы под использование запираемых силовых ключей, скорректирована зависимость B(H) для железа и алгоритм вычисления индуктивности, удалены величины второго порядка малости из дифференциальных вычислений и т.д.). 

Итоговый скрипт позволяет рассчитывать систему с любым количеством одинаковых ступеней и формой магнитопровода и снаряда, соответствующими использованным в проекте Dantista. На рис. 2 показан скриншот работы FEMM для 4-ступенчатого ускорителя и результат расчета для 8 ступеней.

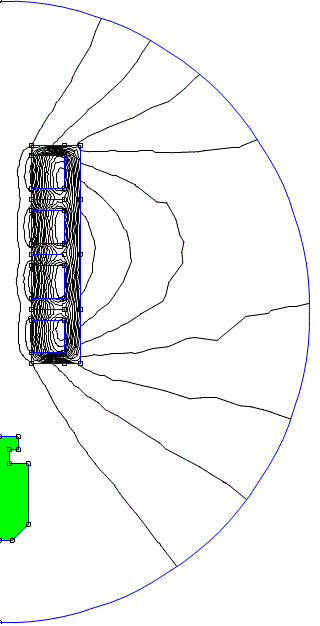Start of simulation 05/25/18 12:04:18 Capacitance, microFarad = 1100 Capacitor resistance Rcc, Ohms = 0.107 Initial Voltage, Volts = 900 External resistance, Ohms = 0.167 Coil resistance, Ohms = 1.19140875 Number of turns = 151.29 Wire diameter, mm = 0.4 Total wire length, meters = 8.55524794586427 Coil length, mm = 6 Outer coil diameter, mm = 24 Number of coils = 8 Coil1 Inductance with projectile in start position, microHenry = 554.7680773168279 Coil2 Inductance with projectile in start position, microHenry = 573.2230165134845 Coil3 Inductance with projectile in start position, microHenry = 575.4581217269606 Coil4 Inductance with projectile in start position, microHenry = 576.4467974758734 Coil5 Inductance with projectile in start position, microHenry = 576.1513718168307 Coil6 Inductance with projectile in start position, microHenry = 575.301429590138 Coil7 Inductance with projectile in start position, microHenry = 571.1674678841667 Coil8 Inductance with projectile in start position, microHenry = 544.7686535787516 Thickness of the core ends, mm = 2 Thickness of the external core tube , mm = 3 Inner coil diameter, mm = 12 Head mass, grams = 10.05404211087609 Head length, mm = 14 Head diameter, mm = 10.8 Cone length, mm = 3 Cone diameter, mm = 5 Tail 1 length, mm = 2.5 Tail 1 diameter, mm = 4 Tail 2 length, mm = 2.5 Tail 2 diameter, mm = 7 Start projectile position in coil, mm = 2 Total time, microsec = 3670.000000000009 Time step,  microsec =10 Muzzle energy, J = 13.85657622572239 Capacitor energy stored, J0 = 445.5 Capacitor energy wasted, J = 69.49520089948786 Efficiency (percent) = 19.93889656605698 Initial projectile velocity, m/s = 2 Out projectile velocity, m/s = 50.56932268545591 Maximal projectile velocity, (in coil), m/s = 50.57523762196579 End of simulation at 05/25/18 13:33:09

 

Рис.2. Скриншот работы модели 4-ступенчатого койлгана (слева) и краткий результат расчета для 8-ступенчатой системы (справа).

 

Полный файл отчета с формами тока в каждой ступени, зависимости координаты снаряда и действующей на него силы от времени и т.д. приведен здесь.Текст скрипта будет мной выложен ниже после получения экспериментальных данных, позволяющих окончательно его верифицировать. 

Замечания:

1) Созданный скрипт является первым приближением, т. к. при расчете разгоняющей силы учитываются токи через все действующие катушки, однако э.д.с. связанная с взаимной индуктивностью катушек не принимается во внимание. То есть учитывается совместное действие нескольких катушек на снаряд, но не на друг друга. В случае DD11, где катушки достаточно удалены друг от друга, а магнитопровод насыщен из-за большой силы тока, влияние взаимных индуктивностей вряд ли приведет к существенной ошибке ( я думаю не более 10 % при определении тока). Но для точного описания таких систем (особенно при малых токах) скрипт надо будет дополнять. Причем усложнение будет значительное, и как оно скажется на скорости расчетов пока непонятно (см. ниже).

2) При разработке скрипта мной были проведены дополнительные исследования, связанные с желанием ускорить его работу при сохранении приемлемой точности результатов. Дело в том, что традиционный способ ускорения работы программы - увеличение шага по времени dt - в данном случае не подходит, поскольку, помимо собственно движения снаряда (которое в первых ступенях действительно медленное и могло бы позволить увеличение dt), скрипт должен моделировать формы тока в катушках, которые меняются с большой скоростью и независимо от положения снаряда в стволе (т. к. все ступени одинаковые). Поэтому значение dt в данном случае ограничено величиной 5..10 мкс.

По изложенным причинам ускорение работы программы достигалось изменением алгоритма вычисления индуктивности катушек (которое занимает максимальное количество ресурсов процессора). Для конкретизации того, о чем здесь говорится, запишем уравнение Кирхгофа для одной из ступеней койлгана:

 

U = i·R + L·(di/dt) + i·(dL/dt)                                                         (1)

 

Здесь в явном виде записана индуктивная э.д.с., зависящая как от производной тока во времени, так и от производной индуктивности (заметим, что обычно ограничиваются только первым слагаемым). Э.д.с. U , стоящая в этом уравнении слева, равна напряжению источника питания, подключенного к катушке (она положительна, когда источник подключен в прямой полярности, и отрицательна, когда полумост переключается в режим рекуперации и ток начинает "втекать" в емкость).

Поскольку индуктивность L = L(i,x) зависит как от положения снаряда x, так и от тока в катушке (т.к. мы имеем нелинейно намагничиваемую среду с магнитопроводом), то производная индуктивности во времени может быть записана как 

 

dL/dt = (dL/dx)(dx/dt) + (dL/di)(di/dt) = v·(dL/dx) + (dL/di)(di/dt)            (2)

 

Здесь v - скорость снаряда.

Подставляя (2) в (1), можно получить уравнение относительно di, которое позволяет вычислить ток на каждом шаге симуляции - так и работает базовый алгоритм, заложенной в существующие скрипты FEMM. Но из вида уравнений (1) и (2) понятно, что, вообще говоря, существует 4 пути, позволяющие провести такие вычисления:

 - с учетом всех слагаемых (частных производных индуктивности по току и координате);

 - с учетом только одного из членов в уравнении (2) (в подавляющем большинстве скриптов, выложенных, например, на соответствующей ветке форума Арсенала, учитывается производная dL/dx);

- без учета вклада в э.д.с. обоих членов в уравнении (2), лишь вычисляя точное значение индуктивности на каждом шаге моделирования для подстановки в (1);

- вообще без учета изменения индуктивности во времени (т. е. индуктивности катушек считаются постоянными и равными начальным значениям, вычисляемым при старте работы программы).

Ясно, что трудоемкость (а, следовательно, и длительность) вычислений по этим алгоритмам будет совершенно различной (а именно, уменьшаться в порядке перечисления). Я провел сравнительный анализ скорости вычислений для 4-ступенчатой системы для всех перечисленных вариантов. На рис. 3. показано то, что получилось в результате.

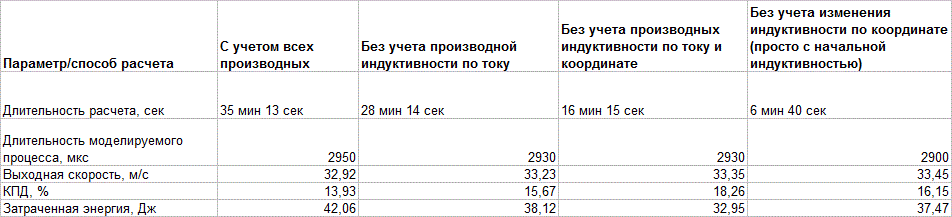
Рис. 3. Результаты моделирования 4-ступенчатой системы койлгана "бегущей волны" по различным алгоритмам.

 

Расчет проводился на обычной офисной машине средней мощности (Intel(R) Core(TM) i3-2100 CPU 3,1 GHz, 4 GB ОЗУ). Как видно, наилучшее приближение к точному результату (за который принимается результат вычисления по первому алгоритму) обеспечивается общепринятым методом, не учитывающим производную индуктивности по току. Правда, и экономия машинных ресурсов при этом минимальна. К моему удивлению, вычисление по максимально упрощенному способу, вообще не учитывающему изменение индуктивности катушек за время выстрела, дает неплохую точность, при этом скорость расчетов увеличивается почти шестикратно! Это говорит о том, что такой метод можно использовать для предварительных вычислений, особенно в случае систем с большими напряженностями полей (где все ферромагнитные части должны быть глубоко насыщены). 

Наконец, можно отметить, что наиболее точный способ расчетов дает самое минимальное КПД и выходную скорость снаряда. При этом обсчет довольно простой 4-ступенчатой системы с шагом времени 10 мкс занял более получаса, а 8-ступенчатой - полтора часа (см. выше). При внесении в скрипт модификаций, учитывающих взаимную индуктивность катушек, следует ожидать еще более значительного снижения скорости расчетов - эту проблему нужно будет как-то решать в дальнейшем.