Поскольку койлган по определению - это ускоритель ферромагнитного тела, то для описания его свойств сначала надо ответить на ключевой вопрос: чему равна сила, с которой катушка с током притягивает к себе ферромагнетик? Для этого придется немного углубиться тему и вспомнить некоторые вещи из общего курса физики.
В современной теории магнитное поле принято характеризовать двумя величинами - индукцией В и напряженностью H (это вообще говоря векторные величины, т. е. они имеют направление в пространстве, но здесь мы эти сложности пока опустим). Напряженность характеризует поле, генерируемое макротоками (т. е. упорядоченным движением электронов в проводниках), а индукция - суммарное поле, образуемое как макротоками, так и микротоками (т.е. неупорядоченным движением носителей заряда в среде). Связь между ними дается следующим соотношением:
| B = µ·µ0·H | (1) |
где µ - т. наз. магнитная проницаемость среды (характеризует способность вещества к магнитной поляризации, т.е. ориентации микротоков под воздействием внешнего поля), а µ0 - коэффициент пропорциональности, который в разных системах исчисления имеет разное значение и размерность, и имеет смысл магнитной проницаемости вакуума. В системе СИ напряженность измеряется в Амперах на метр (А/м), индукция - в Тесла (Тл), а µ0 ≈ 1,26·10-6 Гн/м.
У большинства веществ (парамагнетиков, диамагнетиков) значение µ весьма мало отличается от единицы, т.е. микротоки слабо реагируют на внешнее поле, и сила их взаимодействия с магнитом ничтожна (хотя и может быть обнаружена в разных интересных опытах). Ферромагнетики (самый распространенный из которых - железо) устроены по-другому - в них области, в пределах которых микротоки имеют одно направление (они называются домены) могут упорядочиваться и объединяться таким образом, что даже при слабом внешнем воздействии суммарная индукция поля в веществе резко возрастает. Этот процесс хорошо проиллюстрирован на следующих картинках (две последние взяты с сайта Джеймса Пола):
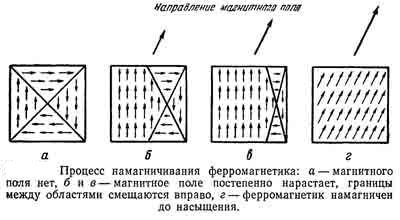 |
Изменение границ доменов при намагничивании железа |
 |
Неупорядоченные микротоки ферромагнетика при отсутствии внешнего поля |
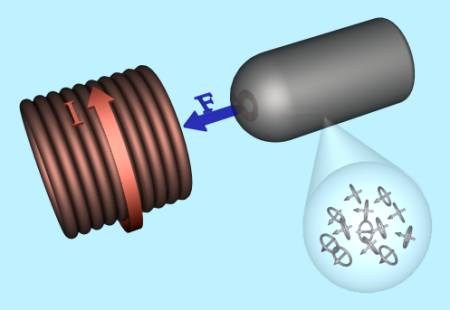 |
Упорядочивание микротоков |
Рис. 1. Иллюстрация процессов при намагничивании ферромагнетика.
В результате магнитная проницаемость ферромагнетика приобретает вид, показанный на рис. 2 слева, а индукция поля - там же справа. Как видно, при намагничивании внешним полем за счет переориентации доменов сначала происходит резкий рост индукции, при этом значение магнитной проницаемости может достигать нескольких тысяч. Затем (это происходит при величинах порядка H ~102 Ампер/метр), когда почти все домены уже "выстроились" вдоль поля, µ начинает спадать. Такое состояние ферромагнетика называется "насыщением" и характеризуется величиной индукции Bнас. После насыщения индукция поля при увеличении H продолжает расти, но уже "обычным" образом, т. е. за счет внешних токов.
 |
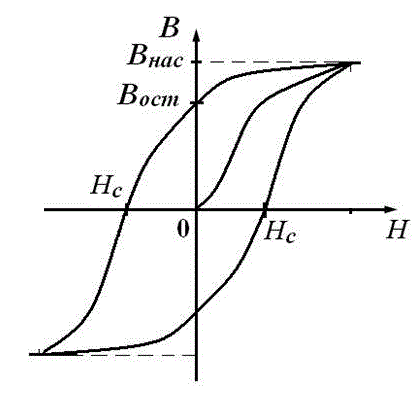 |
Рис. 2. Зависимость магнитной проницаемости (слева) и индукции (справа) от напряженности поля. Показаны индукция насыщения Bнас, а также остаточная индукция Вост (она характеризует поле доменов, которое остается после исчезновения внешнего воздействия). Для ее подавления необходимо приложение дополнительного поля, которое называется "коэрцитивной силой" ферромагнетика Нс.
Для более наглядного понимания этих процессов можно переписать выражение (1) следующим образом:
| B = (1+x) ·µ0·H = µ0·H + µ0·M | (2) |
где x - т. наз. "магнитная восприимчивость" (x = µ -1), а М - вектор намагниченности среды (M = x·H).
Из этой формулы ясно видно, что индукция магнитного поля внутри вещества образуется как внешним полем, так и полями микротоков среды. При этом в довольно слабых полях (до и вблизи насыщения) в ферромагнетике µ >>1, поэтому первым слагаемым в (2) можно пренебречь (т. е. индукция почти полностью формируется полями микротоков и близка к Bнас = µ0·Mнас, где µ0·Mнас - намагниченность насыщения). В очень сильных полях ( > 106 А/м), наоборот, намагниченность среды сравнительно мала - ферромагнетик ведет себя как "обычное" вещество, и поле в нем определяется внешними источниками.
Если теперь, наконец, закончить с физическими основами и перейти к предмету нашего рассмотрения - койлганам, то нужно сказать, что поля в них обычно попадают как раз в "средний" диапазон значений (т. е. составляют порядка 105 А/м).Этот момент осложняет рассмотрение, поскольку любые упрощения, на которые обычно идут при теоретическом анализе гауссовок (например, приравнивая индукцию поля в снаряде индукции насыщения, или наоборот, считая µ ≈ 1), можно принять лишь с большой погрешностью. Точный результат может дать лишь моделирование в пакетах типа FEMM, но мы-то хотим получить аналитические приближения, поэтому придется идти на определенные компромиссы.
Теперь у нас есть необходимая теоретическая база, чтобы ответить на вопрос, вынесенный в заглавие этого раздела.
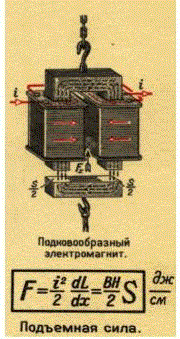
Вначале остановимся на одном общеизвестном соотношении, которое можно найти литературе по магнетизму. В [1] приведена следующая формула для силы притяжения железного сердечника к электромагниту:
| F = ½ B·H·S | (3) |
где S - площадь сердечника, перпендикулярная магнитному потоку, H - напряженность поля на поверхности сердечника, обращенной к полюсу магнита.
Пара картинок, иллюстрирующая это соотношение, показана на рис. 3
 |
 |
Рис. 3. Подъемная сила магнита.
Эта формула относится к случаю, когда воздушный зазор между сердечником и магнитом мал, и магнитный поток полностью замыкается через сердечник (т. е. снаружи него поля нет). Кроме того, неявно предполагается, что работа идет на линейном участке зависимости B от H до насыщения (отсюда, например, берется множитель ½). Ясно, что наш случай намного сложнее, ведь поле у нас очень сильное, а какая-то его часть рассеивается вне ускоряемого тела.
Чтобы получить более точное соотношение для койлганов, изобразим схематически катушку с током, втягивающую в себя железный снаряд длиной l и площадью S (см. рис. 4). На рисунке красным цветом также показана зависимость напряженности поля, создаваемого катушкой, от координаты (будем считать, что поле постоянно во времени и однородно по радиальному сечению снаряда, т.е. изменяется только вдоль оси Ох).
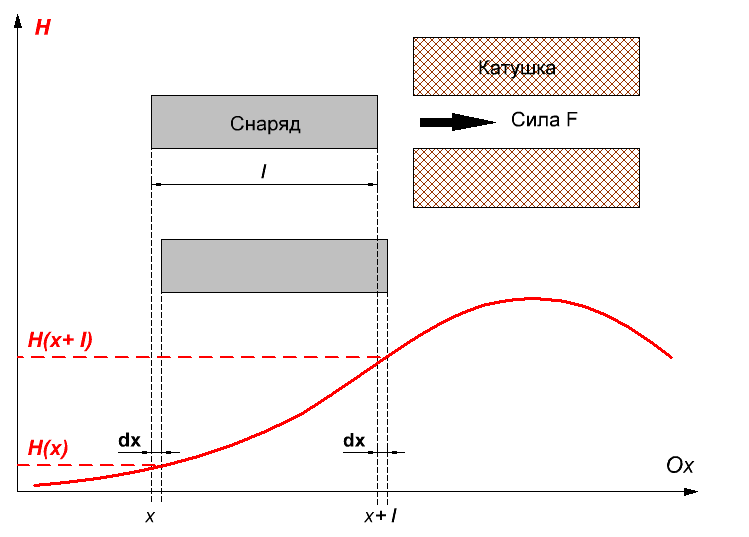
Рис. 4. Иллюстрация для вычисления силы, действующей на снаряд в койлгане.
Физика нам говорит, что сила, действующая на тело, численно равна производной энергии системы по координате, т.е. отношению изменения энергии при перемещении тела на бесконечно малую величину dx, к этому самому dx:
| F = - dW/dx | (4) |
Из рис. 4 видно, что изменение энергии нашей системы при смещении снаряда на dx имеет место только в двух местах - на переднем и заднем торцах снаряда. Его можно представить себе так, как будто с заднего торца срезают тонкой слой толщиной dx и переносят вперед на величину l (при этом напряженность внешнего поля для него изменяется с H(x) до H(x+ l)). При этом такой же слой воздуха переносится с переднего на задний конец снаряда. Если считать, что снаряд слабо искажает пространственное распределение силовых линий (что должно быть правдой в сильных полях), то во всем остальном объеме вокруг катушки никаких изменений не происходит, т. е. там dW = 0.
Далее, известно (см. например [3]), что изменение плотности энергии магнитного поля в веществе при вариации индукции имеет следующий вид:
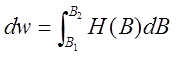 |
(5) |
Таким образом, общее изменение энергии системы будет равно суммарному изменению энергии в ферромагнетике объемом dx·S при при перемещении его из поля с индукцией B(x) в поле с индукцией B(x+ l), и в слое воздуха того же объема, который перемещается между этими же точками пространства в обратном направлении:
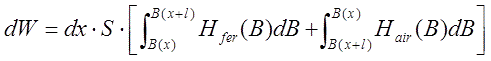 |
(6) |
Здесь Hfer(B), Hair(B) - зависимость напряженности от индукции для ферромагнетика и воздуха, соответственно. Визуально это ситуация показана на рис. 5, где схематично изображены ход индукции для железа (сплошная линия) и воздуха (пунктирная линия). Изменение энергии ферромагнетика выражается площадью заштрихованной фигуры.
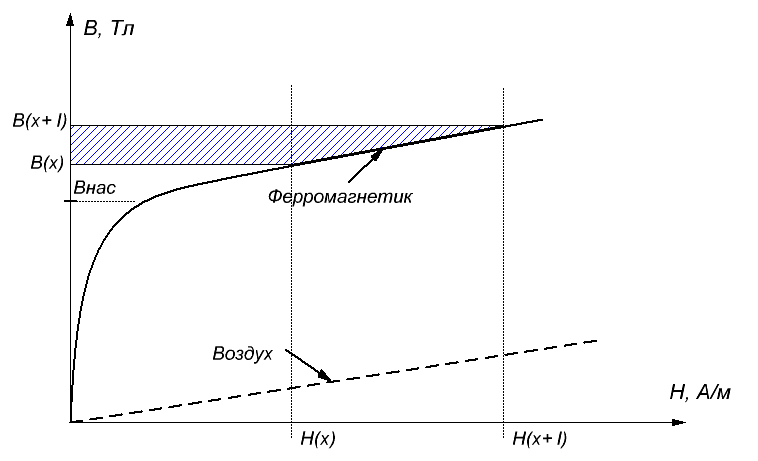
Рис. 5. Зависимости B(H) в ферромагнетике и воздухе. Как видно, в сильных полях зависимости идут практически параллельно со сдвигом на величину Bнас.
Зависимости H(B) для интересующих нас материалов можно выразить из формулы (2) с той только разницей, что в воздухе второе слагаемое (намагниченность материала) равно нулю.
Тогда для действующей силы получим, наконец, следующее соотношение:
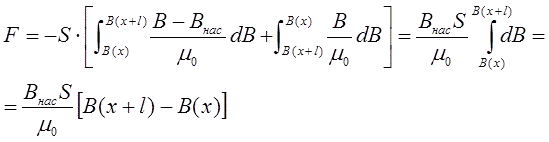 |
(7) |
Выражая индукцию через напряженность (1), получим окончательно:
| F = Bнас ·S ·[H(x+ l) - H(x)] | (8) |
Простота этой формулы в том, что все величины в ней могут быть легко подсчитаны - площадь сердечника (снаряда) выбираем мы сами, индукция насыщения для разных ферромагнетиков тоже хорошо известна, а напряженность поля H катушки с током может быть просто определена с помощью того же FEMM или аналитических соотношений, которые приведены, например в [2], или в одной из следующих статей этого раздела.
Подобный результат можно получить, если представить наш снаряд в виде магнитного диполя с моментом P. Тогда сила воздействия магнитного поля на снаряд приобретает вид, который приведен на сайте Д.Пола :
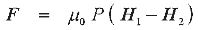 |
(9) |
где H1, H2 - напряженности поля на переднем (ближнем к катушке) и заднем торцах снаряда, соответственно. Иллюстрации даны на рис. 6 (взято с той же страницы)
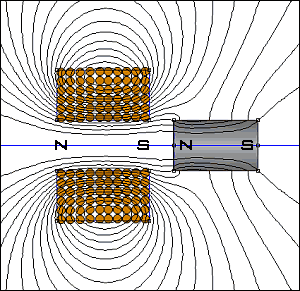 |
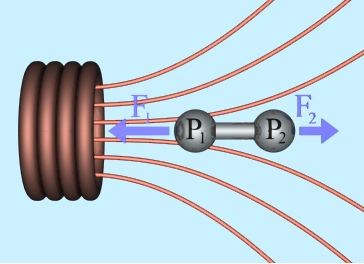 |
Рис. 6. Представление силы, действующей на снаряд койлгана, как втягивания постоянного магнита в катушку с током.
Таким образом, в первом приближении мы ответили на интересующий нас вопрос: сила втягивания сердечника в электромагнит приблизительно пропорциональна разнице напряженности поля на его переднем и заднем торцаx.
Из этого вывода ясно, что для оценки параметров катушечного ускорителя критически важно уметь вычислять напряженность поля, создаваемую его обмоткой (или обмотками если речь идет о многоступенчатой системе). Этой задаче посвящены следующие публикации этого раздела.
Литература:
[1] Зильберман Г. Е., "Электричество и магнетизм", М., "Наука" 1970 г., 384 стр.
[2]. Карасик В. Р., «Физика и техника сильных магнитных полей», М., "Наука" 1964 г., 348 стр.
[3]. Арнольд Р. Р., "Расчет и проектирование магнитных систем с постоянными магнитами", М., "Энергия", 1969, 184 стр.
Дополнение от 10.09.2020: для подтверждения аналитического соотношения (8) проведен расчет в FEMM . Его процедура и результаты выложены здесь. Для сильных полей, которые имеют место в электромагнитных ускорителях масс, соотношение можно считать доказанным.
| Вперед> |