<Назад

Вперед>

 

3. Максимальное значение кинетической энергии снаряда.

Попробуем теперь понять, к чему нас приводят соотношения (12) и (14), полученные на предыдущей странице.

Во-первых, оценим максимальную энергию, приобретаемую при втягивании в катушку фиксированных габаритов для снарядов различной длины. Для этого зададимся калибром снаряда (внутренним диаметром катушки) d = 1 см и рассмотрим "идеальную" обмотку с размерами D = 3 см, c = 2 см (при таких параметрах в центре обмотки при данной мощности тока P будет генерироваться максимальное поле). Положим также P = 10 000 Вт (это соответствует току 100 А при напряжении 100 В, т. е. койлгану средней мощности). Тогда для медного провода ( δ ≈ 0,0175 Ом·мм²/м) намотанного без зазоров (a = 1) получим следующие графики:

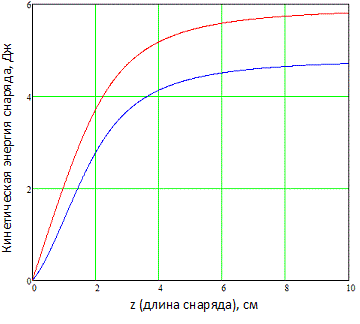Рис. 4. Зависимость кинетической энергии от длины снаряда для случаев, когда передняя грань снаряда в момент начала ускорения находится на бесконечном удалении от катушки (—) или совпадает с торцом катушки (—). Эти случаи соответствуют величинам Emax и E0 в формуле (12).

 

Как видно, при разгоне от торца приобретаемая энергия заметно меньше, чем при старте "из бесконечности".

Кроме того, энергия сначала резко, потом более плавно, но монотонно возрастает при увеличении длины снаряда. По здравом разумении, это вполне логично, поскольку ускоряющая сила (1) пропорциональна разности напряженности поля на передней и задней гранях снаряда, и при удалении задней грани от катушки (читай - увеличении длины снаряда) она растет. Таким образом, если целью ускорения какого-либо тела является получение максимальной кинетической энергии, его длину нужно увеличивать.

С другой стороны, из графиков видно, что энергия в каждом случае стремится к некоторому максимальному значению, которое соответствует снаряду, имеющему бесконечную длину. Эта величина абстрактная, но ее интересно получить в явном виде, т. к она показывает предельную кинетическую энергию, которую можно получить, разгоняя ферромагнетик в данной конкретной катушке. Для этого достаточно снова воспользоваться формулой (9), положив x₂ = -∞, z = ∞ (при этом в "геометрической" функции (10) первое слагаемое в подинтегральных  скобках можно отбросить, т.к. оно станет равным нулю). Поскольку длина снаряда z у нас теперь равна бесконечности, то логично рассмотреть зависимость энергии от других геометрических параметров - наружного диаметра D и длины катушки c (остальные параметры менять не будем). Результат расчета для разгона с бесконечного удаления показан на рис. 5.

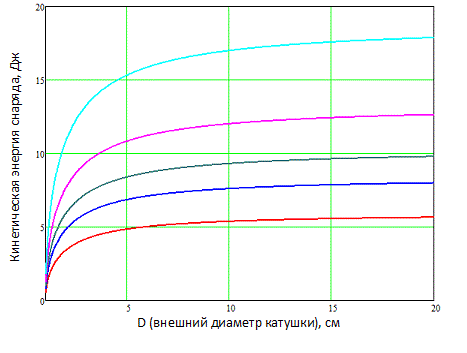Рис. 5. Зависимость кинетической энергии, приобретаемой бесконечным снарядом, от диаметра обмотки различной длины: — - 1 см — - 2 см —-  3 см — - 5 см — - 10 см Разгон начинается с бесконечного удаления от обмотки.

 

Как видно, энергия монотонно повышается с ростом внешнего диаметра и длины катушки. Такой результат понятен: поскольку магнитная проницаемость снаряда падает с ростом напряженности H, то наиболее эффективно втягивать ферромагнетик будет катушка, создающее максимально "размазанное" по пространству поле. Для бесконечно длинного снаряда такой катушкой будет являться, соответственно, обмотка неограниченных размеров...

На рис. 6. показан аналогичный результат для ситуации, когда разгон снаряда начинается от торца катушки. Для удобства изображение дано в логарифмическом масштабе по горизонтальной оси.

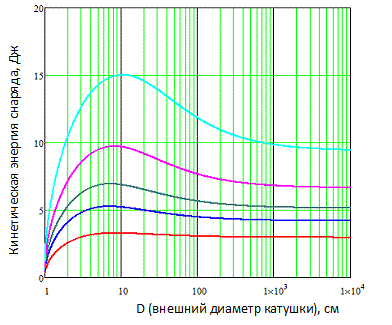Рис. 6. То же, что на рис. 5 при условии разгона от торца катушки.

 

График отличается от предыдущего тем, что для каждой длины катушки теперь имеется максимум на зависимости E(D), т. е. имеется некий оптимальный диаметр обмотки, обеспечивающий наиболее эффективное ускорение сердечника.

Зависимости на рис. 5 и 6  для каждой фиксированной длины обмотки при неограниченном увеличении D стремятся к какой-то определенной величине энергии. Ее, в принципе, можно вывести аналитически, устремив в соотношении (12) диаметр обмотки к бесконечности (D →∞). Поскольку мы сейчас обсуждаем абстрактный случай бесконечного снаряда, я не стал этим утруждаться, но заинтересованный читатель может попробовать проделать эти вычисления самостоятельно. Здесь лишь можно отметить, что эта предельная кинетическая энергия, приобретаемая при разгоне "из бесконечности" , вдвое больше, чем для катушки той же длины получается при разгоне "от торца".

 

В следующем разделе мы рассмотрим более приближенные к реальной жизни случаи снаряда ограниченных габаритов - для них оказывается возможным оценить приращение не только энергии, но и скорости.

 

4. Зависимость скорости снаряда от его размеров и габаритов катушки.

Для начала изобразим приращение скорости снаряда, вычисленное по соотношениям (14), в зависимости от его длины для двух рассмотренных выше случаев - разгона "из бесконечности" или "от торца катушки", причем рассмотрен как случай начальной скорости равной нулю, так и 100 м/с.

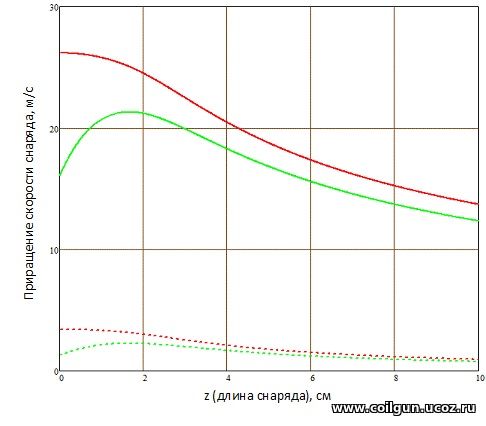Рис. 7. Зависимость приращения скорости снаряда от его длины при разгоне: — - из бесконечности — - от торца катушки Пунктиром даны величины при начальной скорости 100 м/с. Мощность тока 10 000 Вт, наружный диаметр обмотки 3 см, внутренний 1 см, ее длина 2 см.

 

Сразу можно заметить, что при ускорении "из бесконечности" получается максимальное приращение скорости - это хорошо соответствует предыдущим графикам, для которых в этом случае кинетическая энергия также наибольшая. Важной деталью здесь является тот факт, что скорость метаемого тела растет при уменьшении его длины, и для бесконечно короткого снаряда она максимальна.

При перемещении стартовой координаты ускорения к торцу обмотки на зависимости скорости от длины снаряда появляется выраженный максимум, т. е. для данных габаритов обмотки существует оптимальная длина ускоряемого тела, при котором оно получает наибольшую скорость (тем не менее, даже в этом максимуме скорость меньше, чем для бесконечно короткого снаряда в предыдущем случае).

Такой же характер имеют зависимости для высокой начальной скорости тела (с тем только отличием, что абсолютные значения приращения скорости здесь, конечно, меньше).

Если теперь проварьировать габариты обмотки, то получим серию графиков, которые я приводил в публикации, посвященной общим свойствам катушек электромагнитных ускорителей. Здесь рассмотрение ограничено реалистичным случаем ускорения "от торца катушки" из состояния покоя.

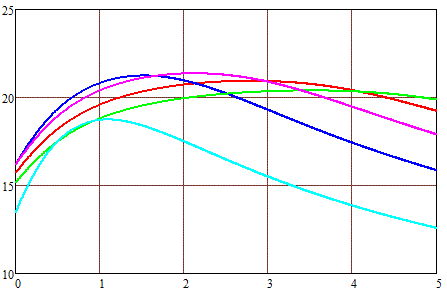
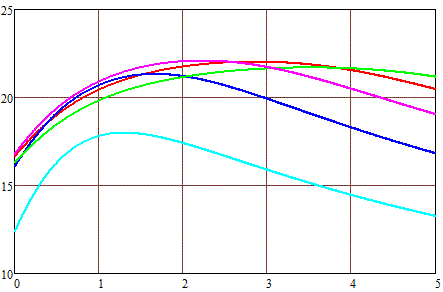
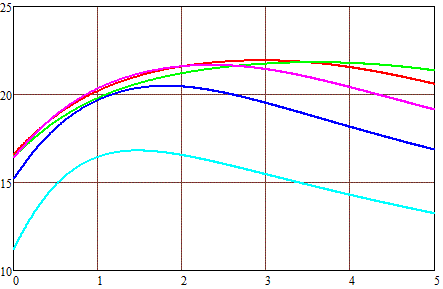
(а)	Рис. 8. Максимальная скорость снаряда калибром 1 см (по вертикальной оси) в зависимости от его длины (по горизонтальной оси). Наружный диаметр обмотки 2 см (а), 3 см(б) и 4 см (в).
(б)	Длина катушек: — - 1 см — - 2 см — - 3 см — - 4 см — - 5 см
(в)

Картина тут аналогичная - для каждого габарита обмотки существует оптимальная (с точки зрения скорости) длина снаряда. Видно, что она растет при увеличении наружного диаметра и длины катушки. Выходная скорость при этом тоже возрастает, но до определенного предела, а потом опять начинает спадать. То есть, опираясь на семейства кривых на рис. 8, можно для каждой конкретной формы снаряда определить габариты обмотки, придающие ему максимальную скорость. Или же наоборот, зная геометрию катушки и координату начала ускорения, можно рассчитать оптимальную длину сердечника.

Наконец, можно заметить, что эта самая оптимальная длина снаряда всегда немного меньше, чем длина соответствующей катушки (если только не рассматривать совсем толстые и короткие обмотки, которые и так далеки от идеала эффективности). Это хорошо коррелирует с результатами моделирования, показанным мной здесь для койлганов малой и средней мощности.

 

В завершение этой публикации я продемонстрирую, как с помощью предложенного подхода можно оценить предельную скорость снаряда, достижимую в койлгане (вне зависимости от его конструкции), имея данные о мощности источника питания.

 

<Назад

Вперед>