Как я упоминал здесь, помимо основной обсуждаемой на этом сайте конструкции электромагнитных ускорителей масс (а именно: ферромагнитный снаряд втягивается обмоткой с током) существует еще множество их конфигураций. В первой половине  XX века наиболее широко исследовалась разновидность индуктивного ускорителя, в которой одна катушка отталкивалась или притягивалась другой. Одна из публикаций, посвященных исследованию такой конструкции, выложена в моем архиве. По некоторым причинам мне в моей деятельности стало интересно изучить этот процесс, для чего я прошел проторенной дорожкой моделирования в FEMM - благо, эта программа обладает всеми необходимыми для этого возможностями.

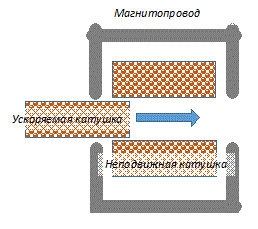
На сайте Петровича есть готовый скрипт для расчета индукционного ускорителя, но он, по сути, моделирует традиционный койлган, в котором железный сердечник заменен на катушку, соединенную последовательно с втягивающей обмоткой, снаружи которой может помещаться магнитопровод  (см. рис. 1 слева). Между тем, реальные конструкции чаще всего устроены по-другому - в них две близкие по диаметру кольцевые обмотки отталкиваются друг от друга, двигаясь поверх центрального магнитопровода (рис. 1 справа).

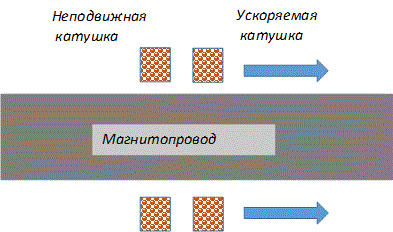Рис 1. Индуктивный ускоритель, моделируемый скриптом Петровича (слева), и тот, который мне был нужен (справа).

Поэтому я решил написать собственный скрипт "с нуля".

Кроме всего прочего, хотелось ввести в него учет всех факторов, в том числе вычисление зависимости индуктивности катушек от протекающего тока в нелинейной системе (т. е. при наличии ферромагнитного сердечника). Поясню подробнее, о чем идет речь.

Запишем уравнение Кирхгофа для одной из ступеней электромагнитного ускорителя (неважно какой конструкции):

U = i·R + L·(di/dt) + i·(dL/dt)                                                         (1)

Cуммарная индуктивность системы L зависит от количества и способа подключения катушек.

В нашем конкретном случае (две последовательно включенные отталкивающиеся обмотки с собственными индуктивностями L₁ и L₂, в которых протекает одинаковый по модулю разнонаправленный ток i ) L = L₁ + L₂ - 2·M, где М  - взаимная индуктивность катушек.

В (1) в явном виде записана индуктивная э.д.с., зависящая как от производной тока во времени, так и от производной индуктивности. Э.д.с. U , стоящая в этом уравнении слева, равна напряжению источника питания, подключенного к катушкам.

Поскольку индуктивность системы L = L(i,x) зависит как от координаты x, так и от тока в катушках (т. к. мы имеем нелинейно намагничиваемую среду с магнитопроводом), то производная индуктивности во времени может быть записана как 

dL/dt = (dL/dx)(dx/dt) + (dL/di)(di/dt) = v·(dL/dx) + (dL/di)(di/dt)            (2)

Здесь v - скорость снаряда.

Таким образом, вообще говоря, существует 3 составляющих индуктивной э.д.с (все они имеют размерность Вольт):

- обусловленная изменением тока во времени L·(di/dt)

- вызванная изменением взаимного положения ускоряемого тела и неподвижной катушки  i·v·(dL/dx)

- обусловленная зависимостью индуктивности (даже неподвижной) катушки от тока в ней i·(dL/di)(di/dt)

Последняя составляющая в ускорителе рассматриваемого типа будет отлична от нуля только при наличии дополнительного ферромагнитного сердечника (магнитопровода), в то время как в обычных гауссовках роль такого нелинейного элемента по умолчанию выполняет сам снаряд. Тем не менее, даже для традиционных гауссовок влиянием этого фактора обычно пренебрегают (в свое время я посвятил исследованию воздействия данного эффекта на скорость и точность расчетов в FEMM один из разделов этой публикации). Не стал исключением и скрипт Петровича, о котором я говорил выше.

Разработанный же мной скрипт был призван, в числе прочего, исправить эту ситуацию и для случая индуктивных ускорителей. В нем, в зависимости от наличия /отсутствия сердечника (критерием такового выступает величина диаметра магнитопровода Dmag - если она более 1 мкм, то система уже считается нелинейной), соответствующим образом скорректирована процедура расчета и введено вычисление производной индуктивности от тока на каждом шаге итерации. Помимо всего прочего, в выходном файле приводятся ряды значений индуктивности обмоток, их взаимной индуктивности, а также все три величины индуктивных э.д.с., описанных выше (последняя из них всегда равна нулю, если Dmag < 1 мкм).

По умолчанию, ускоряемая катушка (лайнер) и неподвижная (толкатель) приняты одинаковыми, а длина магнитопровода составляет три диаметра катушек в сторону ускорения, и два - в обратную. При желании и владении FEMM, эти предустановленные параметры можно изменить в теле программы. Кроме обычных геометрических параметров (наружный и внутренний диаметр катушек, диаметр магнитопровода, начальное расстояние между катушками) можно задать также массу Ms дополнительного тела (снаряда), разгоняемого вместе с лайнером - такие разновидности ускорителей часто предлагается использовать для запуска грузов в космическое пространство.

Как результат расчетов, скрипт выдает обычный набор параметров (выходную скорость, КПД) , а также массу катушки и магнитопровода (если он есть).

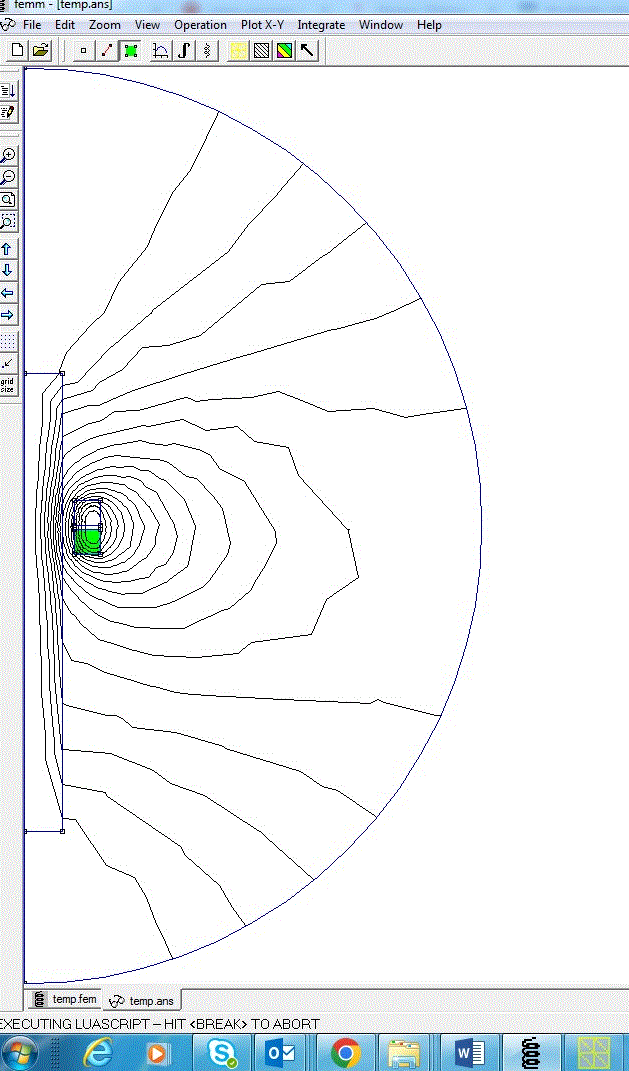
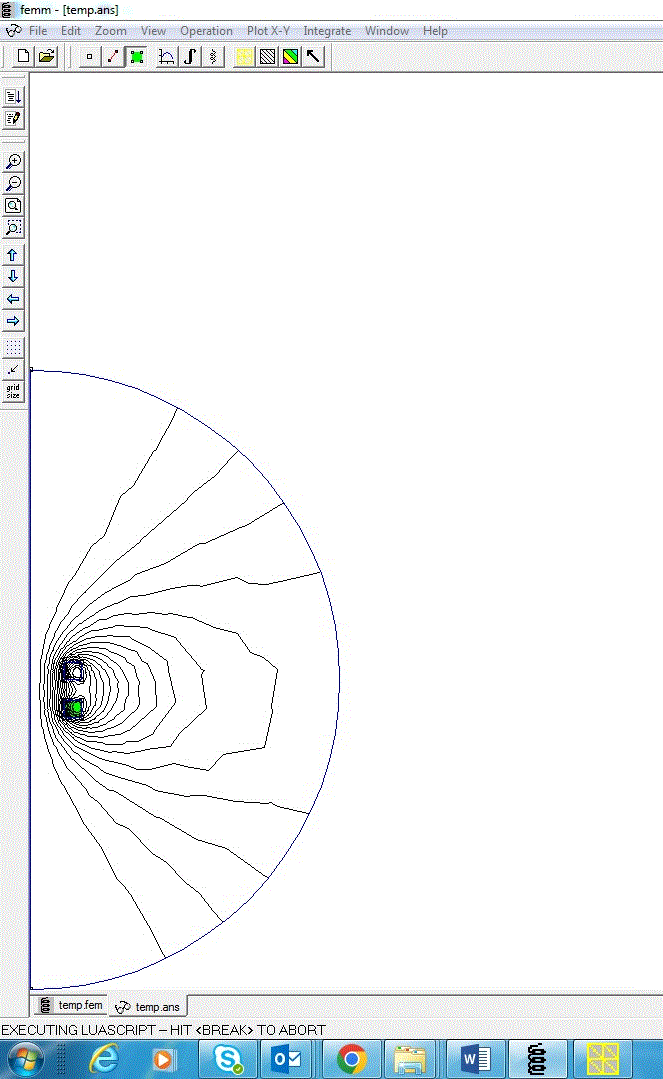
В качестве иллюстрации, приведу результаты расчета зависимости КПД индуктивного ускорителя, питающегося от одного конденсатора 450 В, 470 мкФ. Параметры катушек были такие: диаметр провода по меди 0,5 мм, длина 5 мм, внутренний диаметр 20 мм, наружный 30 мм (при стандартной плотности намотки 0,8 это соответствует массе каждой катушки 9,4 грамм). Расчет был проведен для системы с осевым магнитопроводом диаметром 15 мм, а также без оного.

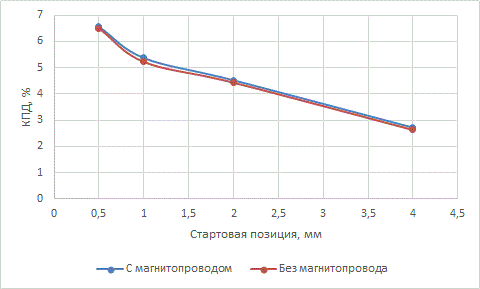Рис. 2. Процесс и результат расчета параметров индукционного ускорителя предлагаемым скриптом.

Сам скрипт можно найти здесь: http://coilgun.ucoz.ru/Inductogun/inductiongun.lua

Как видно, наличие или отсутствие магнитопровода даже при таких небольших энергиях системы влияет на КПД совсем слабо. Это похоже на поведение "традиционных" гауссовок с железными снарядами, но здесь ситуация еще более ярко выраженная, т.к. напряженность поля в индукционном ускорителе, как правило, намного больше, чем в обычном койлгане.

Отличительной чертой индукционных метателей является повышение их КПД с ростом "вкачиваемой" энергии. Я провел несколько симуляций, подтверждающих эту закономерность, но их подробный анализ выходит за рамки данной публикации - возможно, я вернусь к этому вопросу позже.

Всем успехов в творчестве, 

Ваш Eugen.