Данный обсчет посвящен важнейшему вопросу  - какой может быть максимальная эффективность ускорения снаряда в гауссовке?  

Это своего рода "священный Грааль" гауссостроения - каждый конструктор, подбирая параметры своего койлгана, желает знать, как далеко он находится от точки максимального КПД и что нужно сделать, чтобы приблизиться к этому максимуму. Для решения этой проблемы есть два подхода - практический и умозрительный. С практической точки зрения, неоценимую помощь может оказать моделирование в программах-симуляторах типа FEMM. Разработано уже множество скриптов, позволяющих моделировать разнообразные конфигурации электромагнитных ускорителей, в том числе в диапазоне параметров (диаметра провода, начального положения снаряда  и т.д.) - примеры есть на сайте Петровича. Проблема в их использовании состоит в том, что для уверенного определения максимума КПД системы необходимо проварьировать именно все параметры, а не только какой-нибудь один. Например, отыскав оптимальное начальное положение снаряда и соответствующую ему эффективность, исследователь должен убедиться, что он не попал в "локальный" максимум КПД - то есть что при вариации других условий (например, диаметра катушки) ответ не изменится.

В итоге решение задачи оказывается чрезвычайно трудоемким - мне пока неизвестен ни один полноценный расчет на эту тему.

На том же сайте предложен упрощенный алгоритм оценки максимального КПД - снаряд просто фиксируется в точке максимального градиента магнитного поля (которая соответствует максимуму ускоряющей силы), а затем считается интеграл силы по времени действия токового импульса в катушке. Понятно, что такие прикидки довольно далеки от действительности, хотя оценить значение КПД "сверху" они могут.

Теоретический же подход может состоять в следующем. Нам известно, что втягивающая сила пропорциональна изменению индуктивности при движении сердечника (снаряда) в катушке:

                         F = ½ i ² dL/dx                              (1)

Это изменение тем больше, чем большую магнитную проницаемость имеет снаряд. Для ферромагнетиков эта величина быстро падает с увеличением напряженности поля H, поэтому с ростом Н  (т. е. силы тока или, что то же самое, "вкачиваемой" в катушку энергии) КПД системы должно падать.

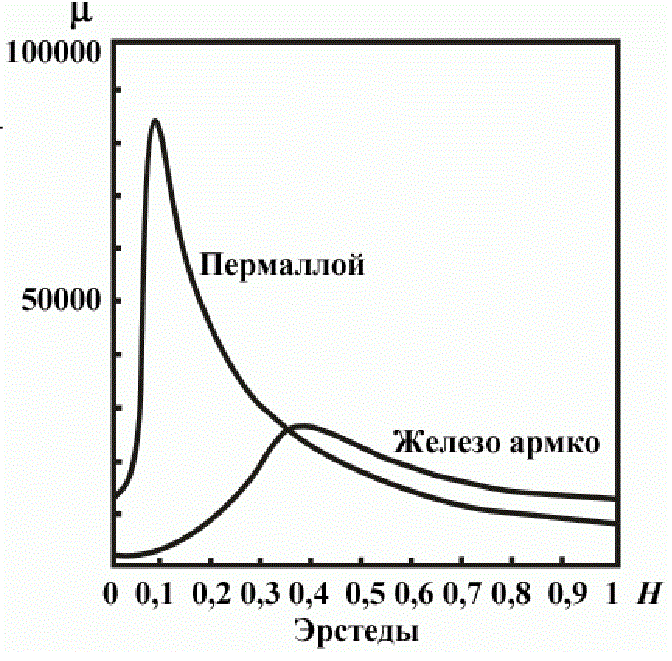Рис.1. Зависимость магнитной проницаемости  ферромагнетиков от напряженности поля.

Такая зависимость действительно наблюдается в подавляющем большинстве случаев, и поэтому снижение энергозатрат на каждой ступени ускорения считается в среде гауссостроителей панацеей для повышения КПД. Затруднений здесь два: практическое и опять-таки теоретическое. Во-первых, понижение энергозатрат эквивалентно снижению приращения скорости снаряда - то есть, он ускоряется хоть и с большим КПД, но медленнее. Поэтому конструктору приходится наращивать количество ступеней и удлиннять ствол, что, рано или поздно, входит в противоречие с ограничениями, свойственными портативной системе (подробнее я анализирую этот момент здесь). Во-вторых, из рисунка выше видно, что проницаемость ферромагнетиков имеет пик в области малых полей, после чего опять стремится к нулю. Из этого следует, что зависимость КПД от энергозатрат также будет иметь немонотонный характер (хотя проявляться это должно только в совсем "слабеньких" системах).

Возможен и другой подход. Известно (см. также здесь и здесь), что эффективность ускорения в койлгане зависит от значения ЭДС, индуцируемой движущимся снарядом в обмотке (так называемой "индуктивной  ЭДС"). Эта ЭДС пропорциональна скорости изменения магнитного потока через катушку, т. е. скорости снаряда:

        e_ind ~ dx/dt                                         (2)

Именно поэтому "скоростные" многоступенчатые гауссовки намного эффективнее своих одноступенчатых собратьев.

Однако, если рассматривать с точки зрения оптимизации КПД первую ступень, в которой начальная скорость сердечника (снаряда) равно нулю, то возникает парадокс: с одной стороны, согласно изложенному выше, мы должны снижать затрачиваемую на выстрел энергию, а с другой, согласно соотношению (2), наоборот, стремиться как можно быстрее ускорить снаряд, что достигается только повышением энергии системы. Таким образом, с этой точки зрения тоже получается, что зависимость КПД от энергии не может иметь простой монотонный характер.

Для подробного исследования влияния энергии на эффективность койлгана мной был проведен большой объем симуляций в FEMM. Объектом изучения служила система с закрываемым ключом (транзистором), для чего был разработан специальный скрипт coilgun_107_trans_ind.lua. Особенностью этого скрипта является то, что он позволяет варьировать максимальное напряжение на транзисторе в момент его закрытия (индуктивный выброс), то есть время спада тока в катушке. Этот параметр важен, поскольку чем быстрее может спадать ток, тем ближе может находиться снаряд в момент выключения к точке нулевой силы (середине катушки), что существенно повышает эффективность ускорения.

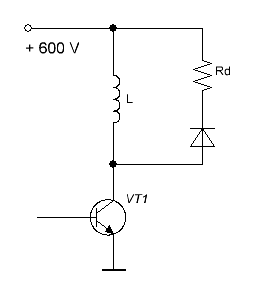Рис. 2. Схема одноступенчатого койлгана, использованного для симуляции.

Так как индуктивный выброс определяется демпфирующим резистором, то в дальнейшем на графиках этот параметр называется "демпфер". Были выбраны два значения "демпфера" - 1200 В (т. е. напряжение на ключе в момент закрытия вдвое превышает начальное напряжение конденсатора), и 2400 В.

Другими варьируемыми переменными системы служили: диаметр провода, наружный диаметр катушки, момент закрытия силового ключа и начальное положение снаряда. Их сочетание и определяло ту величину энергии, которая расходовалась из конденсатора за время выстрела. Всего были взяты несколько точек по энергии: 1 Дж, 3 Дж, 10 Дж, 30 Дж, 100 Дж и 300 Дж. Это позволило построить зависимости в логарифмической шкале, перекрывающей такой большой диапазон энергий.

Остальные параметры были такие:

Начальное напряжение на конденсаторе - 600 В,

емкость конденсатора - 800 мкФ,

паразитное сопротивление системы - 50 мОм,

длина катушки 50 мм

внутренний диаметр катушки 20 мм 

снаряд в виде цилиндра диаметром 18 мм.

Как видно, для анализа был взят довольно крупнокалиберный койлган (это связано с интересом к подобным системам, которыми я на тот момент занимался). На второй итерации я повторил часть расчетов для системы вдвое меньшего калибра, чтобы посмотреть как это повлияет на результат. 

Внизу изображен получившийся график после объединения и обработки результатов в Excel. 

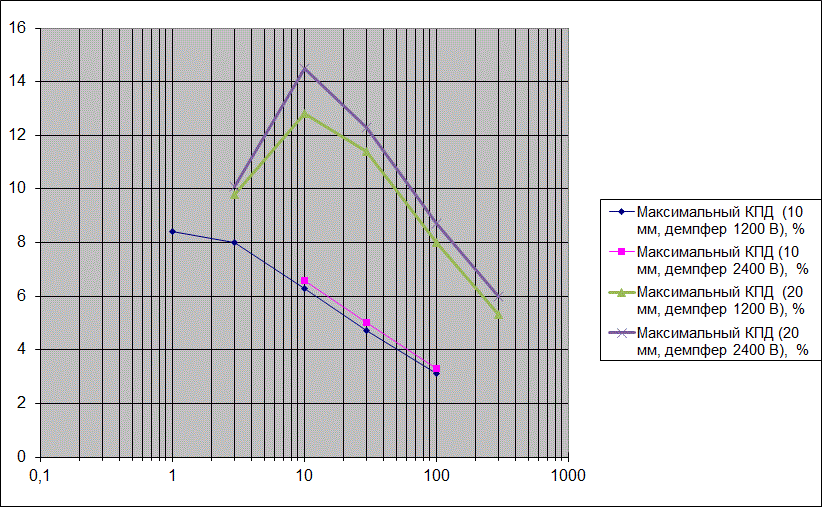
Как видно, главный результат моделирования достигнут: для системы с калибром 20 мм обнаружен пик на зависимости КПД  при энергии порядка 10 Дж. 

Другие важные результаты такие:

1) Для системы диаметром 10 мм, которая ближе к более широко встречающимся в практике койлганам, пик КПД находится вблизи 1 Дж затрачиваемой энергии.  При этом сами максимальные значения КПД имеют порядок 13 % для 20 мм и чуть более 8 % для 10 мм систем, т. е. пиковый КПД растет медленнее ( не пропорционально) калибру койлгана.

2) Значение параметра "демпфер" не слишком существенно влияет на КПД. Это значимый результат, т. .к. позволяет ограничивать допустимое напряжение силовых ключей (что сказывается на их стоимости). Для системы 10 мм я даже не стал проводить моделирование с другой величиной демпфера во всем диапазоне энергий.

3) Зависимость КПД от энергии после прохождения максимума носит ярко выраженный логарифмический характер (эффективность падает обратно пропорционально логарифму энергии).

Всем успехов в творчестве, Eugen