5. Максимальная скорость снаряда, достижимая в одноступенчатом койлгане.

На предыдущей странице было показано, что наибольшая скорость в гауссовке приобретается бесконечно тонким снарядом. Чтобы оценить эту фундаментальную величину, воспользуемся соотношениями (3) и (8), проинтегрировав силу, действующую на "блиноподобный" снаряд бесконечно малой длины dx по траектории ускорения. При этом начальная точка этого ускорения должна быть расположена на бесконечном удалении от катушки (что максимизирует скорость), а конечная -  очевидно, в центре обмотки (т. е., в наших обозначениях, при координате x = -  ½ c ).

 Тогда, в соответствии с (13а), для нулевой начальной скорости имеем:

 

(15)

Интегральное выражение здесь будет равно просто полю в центре катушки (обозначим его как H_m):

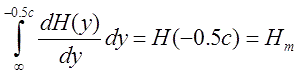
Тогда, заменяя в знаменателе (15) массу снаряда через его геометрические размеры и плотность m = ρ·S·dx, и сокращая площадь S и элемент длины dx, получим  следующее простое выражение:

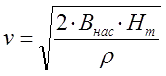(16)

То есть максимальная скорость снаряда зависит только от индукции насыщения материала, его плотности и напряженности поля в центре обмотки.

Если мы говорим о койлгане конкретного калибра d, то можно вспомнить, что наиболее сильное поле генерируется в центре т. наз. "идеальной" катушки, длина которой равна двум внутренним диаметрам, а наружный диаметр - трем внутренним диаметрам. Получается, что именно такая обмотка будет придавать нашему "блину"  максимальную скорость (интересно, что это пожалуй, единственный обоснованный случай, когда "идеальная" катушка действительно обеспечивает гауссовке оптимальные характеристики). Попробуем ее оценить, вычисляя H_m через геометрические параметры и мощность источника по формулам, полученным здесь.

Так, форм-фактор (11) в центре идеальной обмотки (c = 2d, D = 3d, x = - d) вырождается в следующее выражение:

  

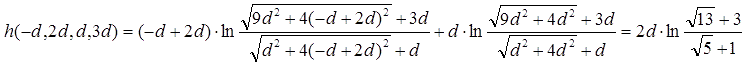
Тогда, подставляя соответствующее значение Н из (5) с учетом его размерности (А/см) в (16), и приводя все численные множители, получим окончательно:

  

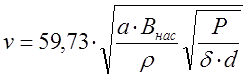(17)

 

Хотел бы еще раз подчеркнуть важность этого соотношения, т.к. оно дают оценку "сверху" для скоростных характеристик (одноступенчатого) электромагнитного ускорителя, вне зависимости ни от габаритов катушки, ни от длины или формы сердечника...

Например, для железного (В_нас = 2 Тл, ρ = 7870 кг/м³) снаряда калибром d = 1 см, ускоряемого медной (δ ≈ 0,0175 Ом·мм²/м) катушкой, намотанной "виток к витку" (а = 1), для источника питания мощностью 10 кВт получим максимальную скорость 26,18 м/с. Эта цифра хорошо коррелирует с результатами, показанными на рис. 7 и 8.

Кроме того, формула (17) позволяет сравнить параметры койлгана по степени их влияния на выходную скорость. Наибольшим "весом" обладают характеристики ускоряемого тела - его плотность и индукция насыщения. Столь же "влиятельной" является плотность намотки а. А вот калибр койлгана и удельное сопротивление провода, которым намотана катушка, оказываются второстепенными параметрами - скорость зависит от них лишь как корень четвертой степени. Причем с увеличением калибра (при сохранении остальных условий) скорость уменьшается. 

Наконец, зависимость выходной скорости снаряда от мощности источника столь же слабая: v ~ P^1/4. То есть, чтобы увеличить скорость снаряда в 2 раза, надо поднять мощность в 16 раз. Например, чтобы получить в вышеобозначенном примере v = 100 м/с, надо иметь источник энергии мощностью ок. 2 130 кВт (эквивалентно току 2130 А при напряжении 1000 В), что близко к пределу даже для современных компактных тиристоров, и намного превышает лимит для управляемых ключей (транзисторов).  Причем, как мы помним, речь идет об "идеальных" условиях (бесконечно тонкий снаряд, ускорение с бесконечной дистанции, т.е. неограниченно долгое) - в реальных системах результат будет намного скромнее...

Это подтверждает давно известный факт того, что для получения высоких скоростей снаряда необходимо использование многоступенчатой системы ускорения. И самое интересное, что с помощью приведенных выше соотношений можно получить оценку для максимальной достижимой скорости и в многоступенчатом койлгане... Этим мы займемся в следующей публикации.

 

 

Всем успехов в творчестве,

Ваш Eugen.

 

<Назад