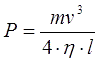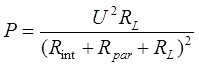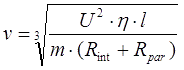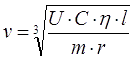| Главная » Статьи » Теоретические статьи » Математика coilgun |
Вступление. В последнее время активно обсуждаются конструкции гауссовок с питанием ускоряющих катушек от аккумуляторов. Среди реально построенных образцов можно выделить койлганы Джейсона Мюррея. Главное отличие от «традиционных» конструкций здесь в том, что нет надобности в зарядке накопительного конденсатора перед каждым выстрелом. При этом, во-первых, становится не нужен соответствующий преобразователь напряжения. Во-вторых, ускоряемое тело может подаваться в тракт ускорителя сразу же после того, как его покинул предыдущий снаряд, и теоретическая скорострельность гауссовки ограничивается только быстродействием системы подачи. Ясно, что главный технический параметр такого койлгана – выходная скорость снаряда – будет зависеть от импульсной мощности, которую способны выдать используемые аккумуляторы. Поэтому разработка портативных аккумуляторных ускорителей стала возможной только с появлением компактных литий-полимерных элементов с высокой токоотдачей. В этой статье я попробую оценить, какая скорость снаряда достижима в «аккумуляторной» гауссовке.
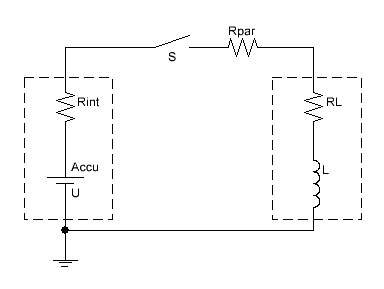
1. Основные соотношение для тока в аккумуляторной гауссовке. Для начала, изобразим электрический контур одноступенчатого койлгана с аккумуляторным питанием (см. рис. 1). Как видно, здесь отсутствует типовой элемент схемы любой гауссовки – накопительная емкость – но явным образом обозначены внутреннее сопротивление аккумулятора Rint (от “internal” – внутренний) и паразитное сопротивление проводников, соединяющих ускоряющую обмотку с элементом питания Rpar (от “parasitic” – паразитный) – они сыграют важную роль в дальнейшем рассмотрении. В паразитное сопротивление включено также и сопротивление силового ключа, коммутирующего катушку (на рисунке он условно изображен в виде переключателя S). Сопротивление провода обмотки равно RL.
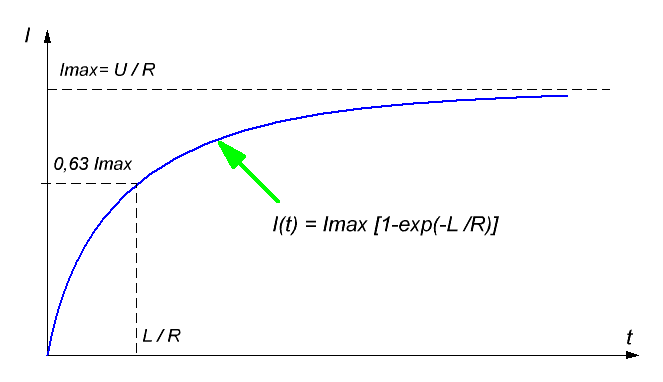
Аккумулятор здесь изображен как последовательное соединение источника постоянного напряжения и его внутреннего сопротивления – это упрощенное представление, но для литиевых элементов в импульсном режиме оно близко к действительности. Таким образом, вместо классического RLC-контура мы теперь имеем более простой RL-контур. Закон изменения его тока после замыкания ключа S хорошо известен и показан на рис. 2. Как видно, ток асимптотически стремится к величине, равной отношению действующего в цепи напряжения к суммарному сопротивлению R = Rint+Rpar+RL: Imax = U / R (1) Принято также вводить понятие «постоянной времени» нарастания тока, которая в данном случае равна τ = L / R (2) За время, равное τ , ток успевает увеличиться до приблизительно 63 % от значения Imax.
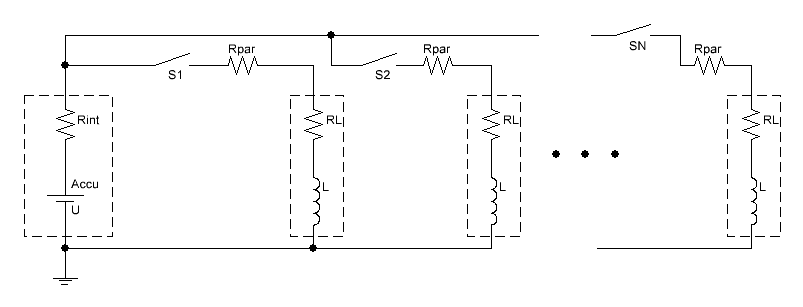
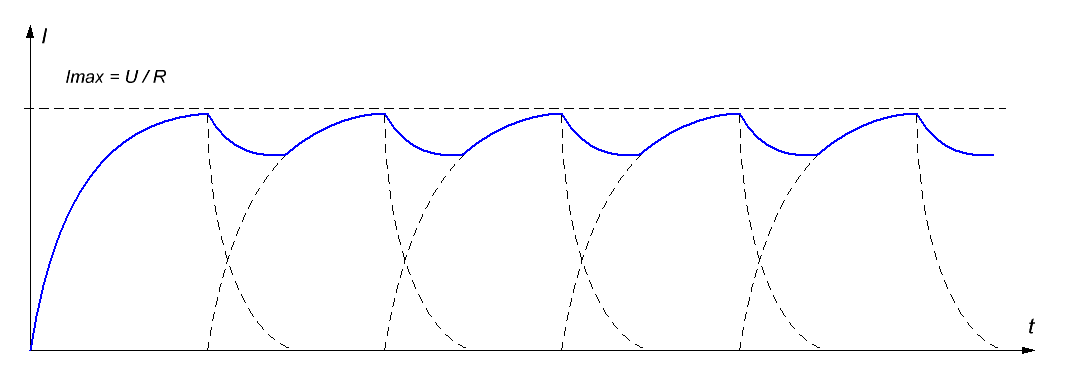
Далее, поскольку максимальная сила тока в цепи соответствует максимальной ускоряющей силе, действующей на снаряд, то в правильно сконструированном койлгане длительность токового импульса в катушке должна быть больше τ, чтобы ток успел достигнуть величины, как можно более близкой к Imax. То есть не будет большой ошибкой, если в дальнейших расчетах пиковую силу тока в цепи койлгана мы будем считать равной Imax. Для многоступенчатой гауссовки этот вывод тоже верен. Действительно, многоступенчатый ускоритель получается из одноступенчатого путем параллельного подключения к источнику питания необходимого количества дополнительных катушек. Для простоты рассмотрения можно считать что все они одинаковые и обладают идентичными параметрами Rpar и RL (тем более, что в упомянутой конструкции Д.Мюррея так оно и есть в действительности). Кроме того, катушки подключаются к аккумулятору по очереди и, как правило, каждая последующая активируется приблизительно в то же время, когда отключается предыдущая. Поэтому можно считать, что сила тока, отбираемого от источника, приблизительно постоянна, и также определяется значением Imax (см. рис. 3).
Роль аккумулятора состоит в том, чтобы обеспечить эту необходимую силу тока.
2. Вывод формулы для скорости снаряда. Напомним, что вопрос, на который мы собираемся ответить, звучит следующим образом: какая предельная выходная скорость снаряда v может быть достигнута в гауссовке, использующей для питания актуальные на сегодняшний день (литий-полимерные) аккумуляторы? В этой заметке я показал, что мощность, необходимая для разгона снаряда массой m до скорости v с КПД η при длине участка разгона l определяется следующим соотношением:
Заметим, что речь идет о мощности, которая выделяется именно на ускоряющей обмотке. Ее значение можно вычислить, если учесть падение напряжения на дополнительных сопротивлениях Rint и Rpar (см. рис. 1):
P = UL· I = [U - I·( Rint+Rpar )] · I
Подставляя сюда выражение для тока (1), получим окончательно для мощности на катушке:
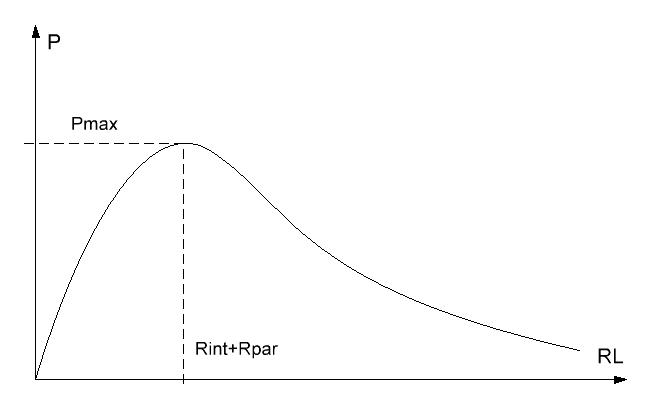
Вид функции P в зависимости от величины RL показан на рис. 4 и хорошо известен из школьного курса физики. Он говорит нам, что максимум мощности на ускоряющей катушке (читай - тока при заданном напряжении источника) достигается, когда сопротивление обмотки равно сопротивлению всех остальных участков цепи, вместе взятых. То есть, наибольшая ускоряющая сила будет действовать на снаряд в том случае, если длина и диаметр обмоточного провода подобраны таким образом, что его сопротивление RL = Rint+Rpar.
При этом мощность P достигает своего максимума, равного Pmax = U 2 / 4 (Rint+Rpar). Сопоставляя это выражение с формулой (3), имеем для выходной скорости снаряда следующее соотношение:
3. Оценка сопротивлений цепи. Из формулы (5) видно, что для определения скорости снаряда надо как-то оценить величины сопротивлений Rint и Rpar, причем желательно прикинуть их минимально возможные значения - тогда мы получим оценку для скорости "сверху". С паразитным сопротивлением цепи все довольно просто - оно определяется сопротивлением открытого силового ключа и соединительных проводников. Сопротивление ключа для современных низковольтных МОП-транзисторов практически ограничено уже не кристаллом (который научились делать достаточно низкоомным), а выводами его корпуса, и составляет, как правило, не более 5 миллиОм (мОм). Еще столько же можно накинуть и на сопротивление проводников - если их изготовить из медных шин достаточного сечения и уделить должное внимание всем соединениям, то получится где-то те же 5 мОм. В итоге можно оценить нижнюю границу для паразитного сопротивления цепи в 10 мОм (т. е. одну сотую Ома). Вероятно, это чересчур "оптимистическая" оценка и в реальной конструкции (особенно с большим стволом, где требуются длинные токоведующие части) Rpar получится повыше, но для нашей цели сгодится. С внутренним сопротивлением аккумулятора все обстоит намного интереснее. Казалось бы, невозможно для всего многообразия типов используемых аккумуляторов указать какое-то единое значение Rint. Действительно, емкость используемых "банок" может составлять от нескольких сотен до нескольких тысяч мА·ч, а напряжение от приблизительно 3,7 В (для 1S-типа, т. .е. одиночного аккумулятора) до 22,2 В (для 6S, т. е. 6 последовательно соединенных элементов). Логично предположить, что и внутреннее сопротивление в этих случаях будет сильно отличаться. Выйти из этого затруднения можно, введя некий коэффициент r, который можно назвать "удельным внутренним сопротивлением" аккумулятора. Его размерность Ом·(мА·ч)/В, а сопротивление произвольного аккумулятора будет выражаться через r следующим образом:
Rint = r ·U / C (6) где U,C - соответственно, напряжение и емкость батареи.
Это соотношение показывает, что внутреннее сопротивление батареи будет расти при повышении ее напряжения и уменьшении емкости. С физической точки зрения такой подход легко обосновать. Действительно, каждая индивидуальная "банка" состоит из собственно активного элемента, генерирующего напряжение (электроды, электролит, сепаратор) и неких соединительных элементов (клеммы), имеющих (в случае фиксированной емкости) более-менее постоянное сопротивление. Соединяя "банки" последовательно, мы повышаем напряжение, но и одновременно пропорционально увеличиваем сопротивление получившейся батареи. Что касается зависимости внутреннего сопротивления от емкости, то теория и практика подтверждают, что она, действительно, приблизительно обратно пропорциональная (как и, например, зависимость ESR электролитических конденсаторов от их емкости). Значение r можно определить из данных спецификаций различных аккумуляторов, например, для такой батарейки емкостью 4000 мА·ч сопротивление одной индивидуальной банки номинальным напряжением 3,7 В составляет около 2,5 мОм, но, с учетом соединений между банками, суммарно получается Rint = 17,9 мОм на батарею из 4 элементов (4S), откуда r = 4·10-3 · 4000 / 3,7 ≈ 4 Ом·мА·ч/В. Эту величину и возьмем для последующих расчетов. Опираясь на выводы этого раздела, формулу (5) можно упростить, если считать, что внутреннее сопротивление аккумулятора преобладает (т. е. Rint>>Rpar). Действительно, в только что рассмотренном примере паразитное сопротивление цепи (которое мы условились считать равным 10 мОм) будет почти вдвое меньше, чем Rint, и это для 14,8-вольтовой батареи, а в реальных конструкциях используются батареи близкой емкости с более высоким напряжением (до 50 В), что приводит к соответствующему росту Rint. Таким образом, в целях упрощения значением Rpar можно пренебречь, и тогда формула (5) с учетом (6) примет следующий вид:
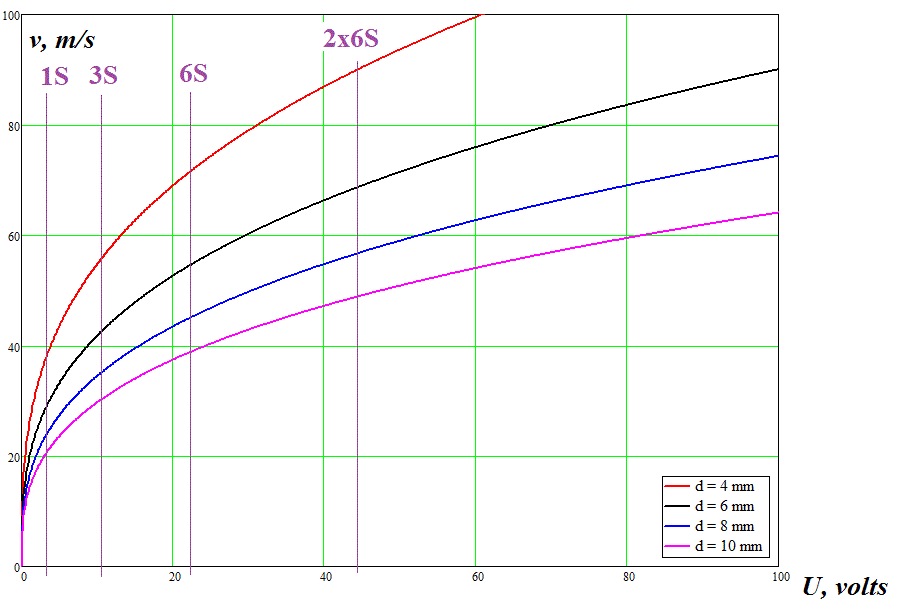
4. Расчет выходной скорости. На рис. 5 продемонстрированы результаты расчета по соотношению (7) выходной скорости снаряда для гауссовки с питанием от аккумулятора емкостью 5200 мА·ч (что близко к пределу для имеющихся в продаже элементов) различного напряжения. Показаны данные для ускорителей различного калибра (d ) от 4 до 10 мм, при этом длина снаряда принималась равной 4d (отсюда вычислялось значение его массы m). КПД, как в предыдущих расчетах, принимался численно равным калибру в миллиметрах (что хорошо совпадает с результатами моделирования и экспериментов для многоступенчатых ускорителей). На шкале напряжений отмечены значения - от 1S (одиночная "банка") до 2x6S (два последовательно соединенных аккумулятора по 6 "банок" в каждом, что дает суммарное номинальное напряжение 44,4 В). Длина разгона (т. е. суммарная длина ускоряющих катушек) принята 50 см.
Рис. 5. Максимальная скорость снаряда для многоступенчатой гауссовки с аккумуляторным приводом, рассчитанная по соотношению (7).
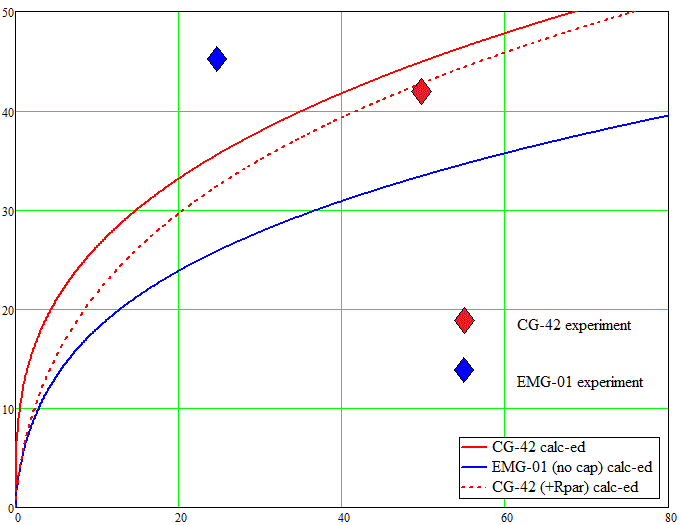
Интересно сравнить результаты расчетов с характеристиками реально построенных аккумуляторных койлганов. На рис. 6 проведено такое сравнение для двух моделей: CG-42 от Д.Мюррея и EMG-01 от ArcFlashLabs (на самом деле, это разновидности одного и того же ускорителя, просто во втором случае между аккумулятором и катушками добавлен шунтирующий конденсатор, о чем подробнее сказано ниже). При расчете учитывались параметры этих койлганов согласно данным автора (см. табл. 1).
Таблица 1. Исходные параметры койлганов для расчета.
Для корректного сравнения данных по койлгану CG-42 наряду с расчетом по упрощенному соотношению (7) использовалась формула (5), учитывающая паразитное сопротивление цепи ≈ 10 мОм (результат такого расчета обозначен пунктирной линией). Экспериментальные данные выведены крупными ромбическими символами.
Рис 6. Сравнение результатов расчета и параметров реальных аккумуляторных гауссовок.
Из графиков видно, что для случая, описываемого ф-лой (5) (т. е. чистый RL-контур без конденсаторов, но с учетом паразитного сопротивления цепи) расчет совпадает с экспериментом очень хорошо. Напротив, добавление в контур дополнительных емкостных элементов резко повышает достижимую скорость снаряда, и вести расчет по полученным нами соотношениям при этом не следует. В следующем разделе проводится краткий анализ полученных результатов.
5. Обсуждение результатов, выводы. Что можно сказать, глядя на полученные результаты? Во-первых, из формул (5) и (7) следует, что выходная скорость снаряда зависит от исходных параметров довольно слабо (как кубический корень). То есть, чтобы увеличить скорость вдвое, надо повысить, например, напряжение батареи в восемь раз. Это говорит о том, что возможности для улучшения характеристик портативных аккумуляторных ускорителей находятся в довольно узких границах. Кроме того, сделанные при расчете v допущения (например, оценка η ≈ d) не должны качественным образом влиять на точность результата. Во-вторых, из графика рис.5 видно, что достижимая скорость растет с уменьшением калибра снаряда (это совпадает с описанными мной свойствами ускорителей других конфигураций). Но даже для минимального в нашем расчете значения 4 мм скорость выше 100 м/с достигается лишь при использовании батареи напряжением более 60 В (эквивалентно использованию трех и более 6S-аккумуляторов, соединенных последовательно), что говорит о высокой стоимости такой гипотетической конструкции. А ведь нужно еще учесть тот факт, что для сохранения длины разгона при уменьшении калибра койлгана необходимо увеличивать количество ступеней (для калибра 4 мм и участка разгона 50 см их число должно быть более 30), каждая из которых оснащена сильноточным полупроводниковым ключом. То есть, создателю аккумуляторной гауссовки с более-менее приемлемыми скоростными характеристиками надо быть готовым к тому, что его детище окажется намного более дорогостоящим, нежели койлганы традиционных конструкций (которые, к слову, уже преодолели рубеж 100 м/с без использования каких-либо особенных технических ухищрений). С другой стороны, высокая скорострельность аккумуляторного ускорителя может компенсировать этот минус. Третье: паразитное сопротивление проводников существенно влияет на параметры койлгана при напряжениях менее 20 В. Так, для рассмотренного случая емкости 3200 мА·ч при учете Rpar скорость снижается вдвое при использовании "однобаночного" аккумулятора, и приблизительно на 10 % при питании от 6 банок (что соответствует падению КПД на ≈ 20 %). Это говорит о том, что нижняя граница используемых аккумуляторов по допустимому напряжению лежит где-то в районе 20 В и соответствует 6S-аккумуляторам. Наконец, характеристики койлгана EMG-01 показывают, что добавление буферной емкости между источником питания и ускоряющими катушками резко увеличивает эффективность системы за счет снятия такого фактора, как внутреннее сопротивление аккумулятора. При этом контур койлгана из рассмотренного RL-типа превращается в "традиционный" RLC с тем лишь отличием, что зарядка конденсатора происходит непосредственно от аккумулятора, а не через преобразователь напряжения (такой тип гауссовок был рассмотрен мной здесь). Данный факт показывает, что "традиционные" конструкции ускорителей с накопительными емкостями пока обеспечивают более высокую эффективность разгона за счет более низкого внутреннего сопротивления конденсаторов (его еще называют ESR) по сравнению с Rint для LiPo аккумуляторов.
Всем успехов в творчестве, Ваш Eugen. | |||||||||||||||||||||||||||||||||||||||||
| Просмотров: 792 | | | |||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |