| Главная » Статьи » Теоретические статьи » Математика coilgun |
В рамках работы над проектами койлганов ЕМ-2 и ЕМ-3 автором этой публикации были проведены некоторые эксперименты и расчеты, закончившиеся созданием неоперенной стрелы для электромагнитного ускорителя. Тем не менее, я заинтересовался этим вопросом, и уже после окончания работы над ЕМ-3 решил провести более подробное исследование, результаты которого и приведены в этой статье. Целью исследования являлось установление соотношений между длиной наконечника и хвостовика неоперенной стрелы (для койлгана или обычного арбалета) и плотностью материалов, из которых они изготовлены. Поясню суть проблемы немного подробнее. Как известно (см. например здесь), аэродинамическая стабильность полета стрелы достигается при определенном соотношении положений центра масс (ЦМ) и центра аэродинамического давления (ЦАД). А именно: расстояние от носика стрелы до ЦАД должно быть, как минимум, в 2 раза больше, чем расстояние от носика до ЦМ. В дальнейшем мы будем рассматривать случай неоперенной стрелы, имеющей равные диаметры хвостовика и наконечника - только такая стрела может использоваться в койлгане, хотя арбалетные болты, как правило, имеют утолщающиеся к концу хвостовики. В этом случае ЦАД находится точно посередине стрелы. Если обозначить длину наконечника как l, длину древка - k·l (т.е. древко в k раз длиннее наконечника), и координату ЦМ относительно заднего торца наконечника как ∆, то получим следующую формулу:
l(1+k) > 4(l+∆) (1)
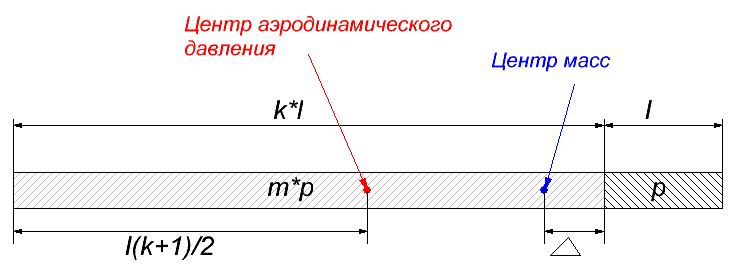
Она проиллюстрирована на рисунке ниже (здесь и далее для простоты наконечник и хвостовик имеют простую цилиндрическую форму). Кроме того, на рисунке обозначена линейная плотность материала наконечника как ρ и линейная плотность материала хвостовика как m·ρ.
Рис. 1. Условия стабилизации стрелы.
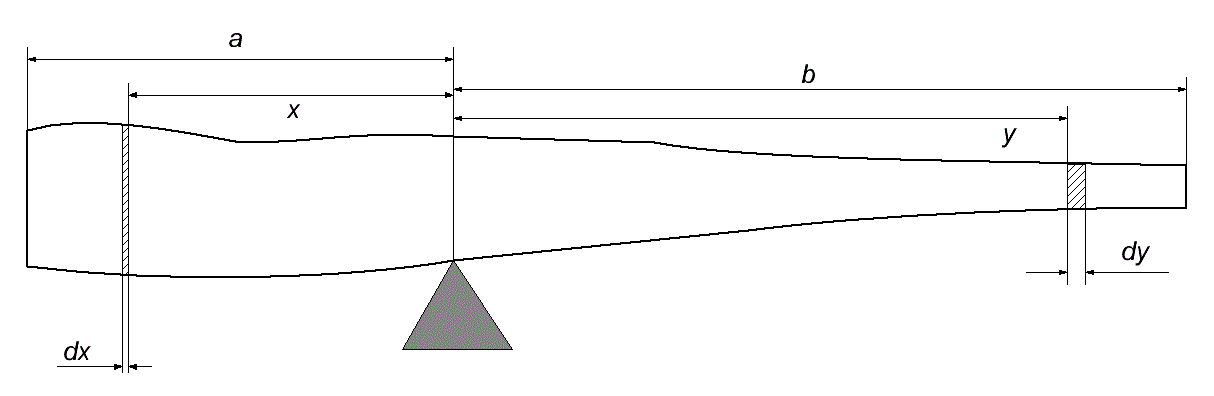
Для того, чтобы двигаться дальше, надо понять, как вычислить точное положение ЦМ. Для этого представим себе вытянутое тело, балансирующее на точечной опоре (см. рис. 2). Здесь изменение линейной плотности тела ρ для наглядности достигается вариацией его диаметра, а не материала, из которого изготовлено тело (как в нашем случае), но сути это не меняет.
Рис. 2. Балансировка тела переменной линейной плотности.
Вспомним школьный курс физики: опора будет находиться в ЦМ, если суммарный момент действующих на нее сил со стороны тела будет равен нулю. Математически это должно быть записано следующим образом:
Применительно к нашему случаю тела постоянного диаметра, собранного из материалов различной плотности (рис.1), это уравнение запишется следующим образом: В том случае, когда ЦМ находится внутри наконечника (т.е. Δ < 0), вид уравнения немного изменится:
Сокращая обе части на ρ и раскрывая определенные интегралы, получим в обоих случаях следующее уравнение относительно Δ:
Таким образом, мы получили соотношение, определяющее координату ЦМ относительно заднего торца наконечника стрелы через длину наконечника, и отношение плотностей (m) и длин (k) наконечника и стабилизатора. Заметим, что, поскольку коэффициенты m и k положительны, знак Δ определяется выражением в числителе. То есть, ЦМ расположен в стабилизаторе (Δ > 0), если и в наконечнике (Δ < 0), если Теперь подставим выражение (4) в (1) и получим следующее квадратное неравенство:
k2·m + k· (3m-1) + 1 ≤ 0 (5)
Как известно из школьного курса математики, условием наличия его вещественных решений является неотрицательность дискриминанта, т.е.
(1-3m)2 - 4m ≥ 0 (6)
Из этого следует, что
(второе решение m >1 является побочным, поскольку, по условию нашей задачи, стабилизатор стрелы сделан из менее плотного материала, чем наконечник). Итак, мы получили важный вывод: плотность материала «древка» (стабилизатора) неоперенной стрелы должна быть в 9 и более раз меньше, чем плотность материала наконечника. Решение неравенства (5) выглядит как диапазон значений относительной длины стабилизатора:
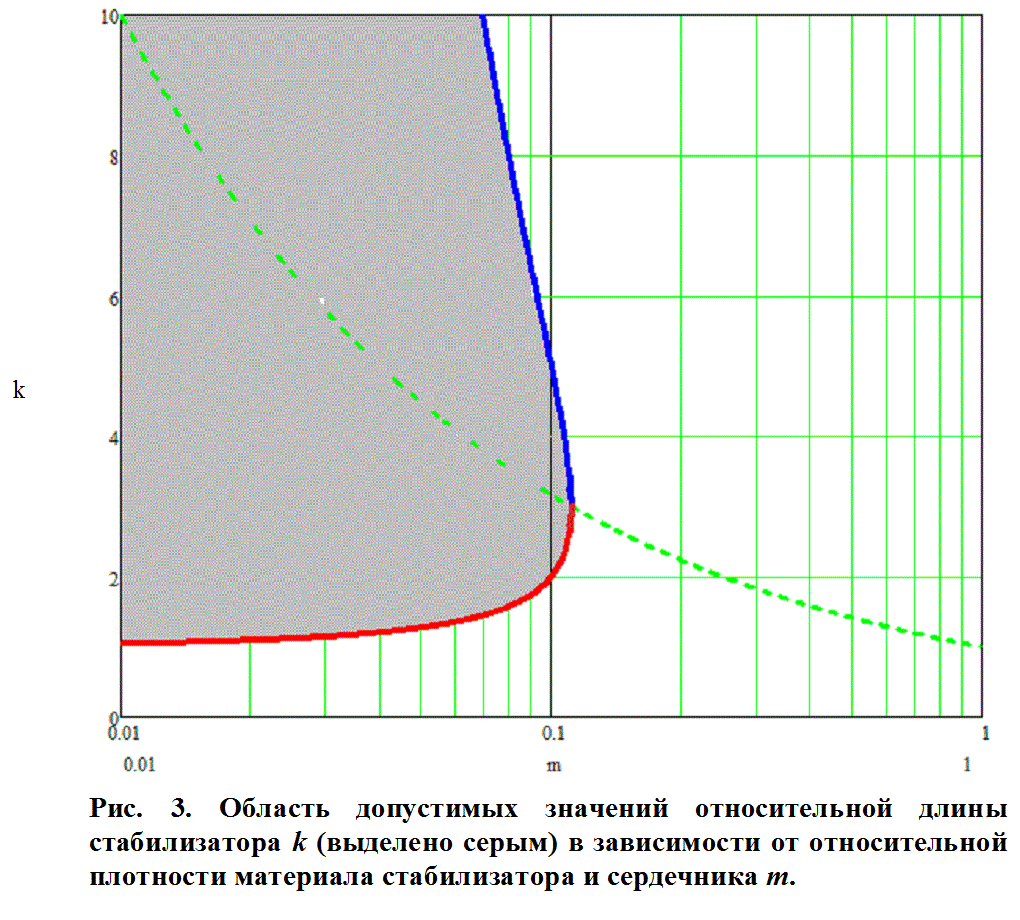
Интуитивно появление этого диапазона понятно – слишком короткая стрела (малое k) не будет аэродинамически стабилизироваться, а при чрезмерном увеличении длины «древка» (большое k) его масса уже будет сравнима и превышать массу наконечника, что приведет к исчезновению выраженного смещения ЦМ в переднюю часть снаряда, которое является обязательным условием стабилизации. Для наглядности проанализируем решение графически:
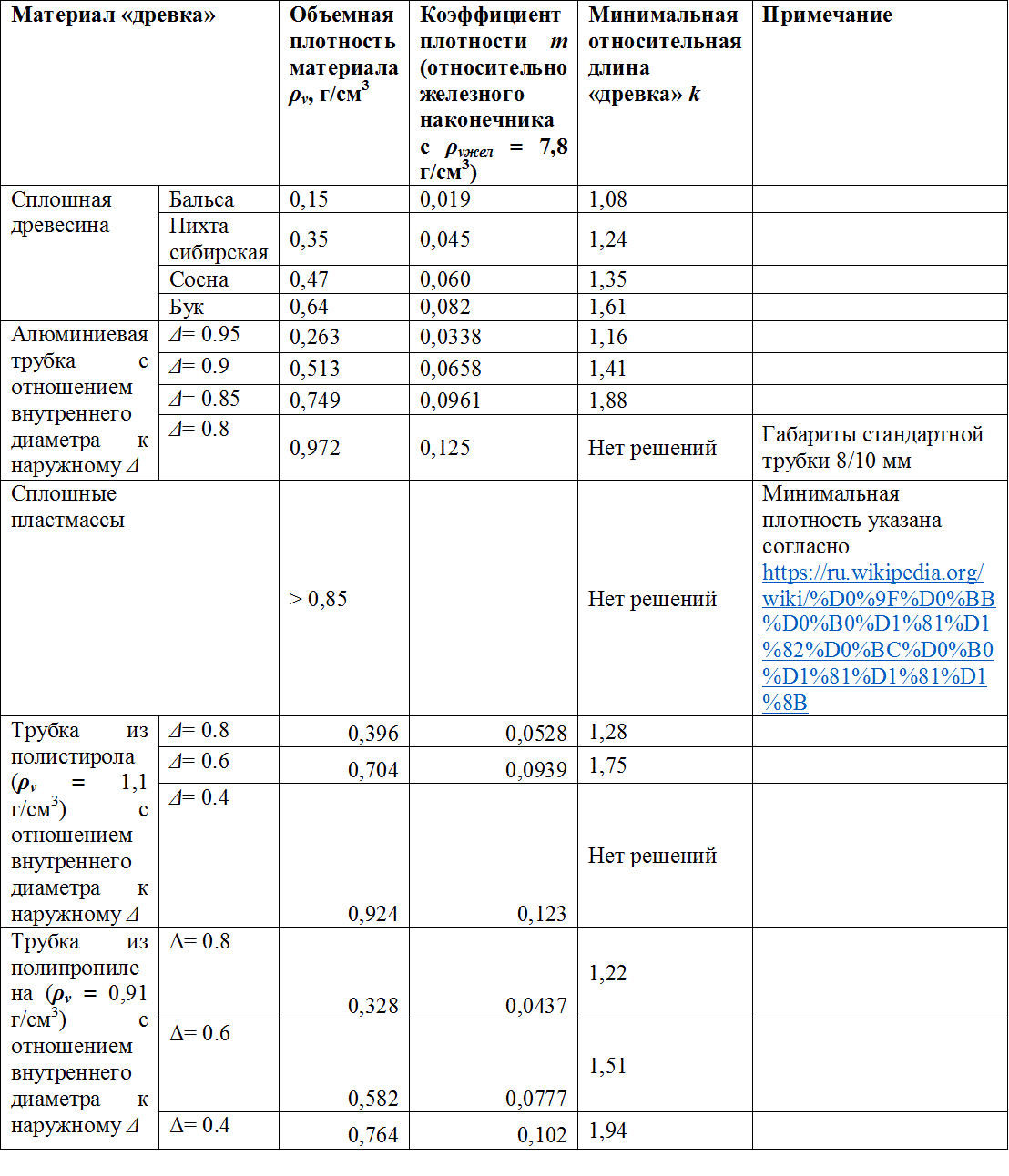
Штриховая линия k=(1/m)1/2 делит область графика на две части – в верхней ЦМ находится за наконечником, в нижней – внутри него. Как видно, при m > 0,11 (в соответствии с (7)), решений не существует, и в этой точке минимальная длина стабилизатора составляет 3 длины наконечника независимо от материалов, из которых они изготовлены. Если говорить об использовании полученных результатов применительно к снарядам электромагнитных ускорителей, то нас, очевидно, должен интересовать случай стрелы наименьшей длины, поскольку при этом «паразитная» масса «древка» будет минимальной – это дает максимально возможный КПД ускорения. В таблице ниже на основании решения неравенства (8) даны минимальные длины стабилизаторов из различных материалов, обеспечивающие стабильный полет стрелы с железным наконечником (в виде значений коэффициентов k).
Таблица позволяет сделать довольно интересные и полезные выводы. Во-первых, выясняется, что для изготовления стабилизаторов стрел (в виде сплошных цилиндров) пригодны практически все сорта древесины (даже такие плотные, как бук). Пластмассы, напротив, не годятся ни одна. То есть сплошное «древко» должно быть именно деревянным :). Во-вторых, если рассматривать трубчатые стабилизаторы, то необходимо принимать во внимание соотношение их наружного и внутреннего диаметра (проще говоря, толщину стенки трубки). При этом получается, что для алюминия это соотношение должно быть больше 0,8, что, например, соответствует стандартной трубке 8/10 мм, широко доступной в строительных магазинах. Для таких трубок меньшего диаметра соотношение диметров получается еще хуже (меньше), из чего следует, что, по крайней мере, для стабилизации снарядов калибром менее 10 мм использовать эти трубки не получится. Характерно, что в качестве стабилизаторов для промышленно выпускаемых лучных и арбалетных стрел (даже оперенных) используются другие, специальные тонкостенные алюминиевые трубки. Что же касается пластиковых трубок, то требования к толщине их стенок оказываются гораздо менее жесткими. Наконец, как видно из таблицы, во всех практически значимых случаях, достаточно длины стабилизатора, равной удвоенной длине наконечника. | |
| Просмотров: 1194 | |
| Всего комментариев: 0 | |
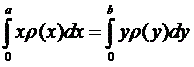 (2)
(2)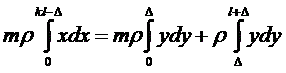 (3a)
(3a)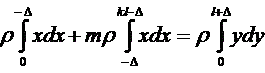
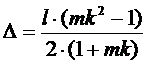 (4)
(4)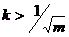
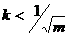
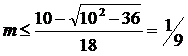 (7)
(7)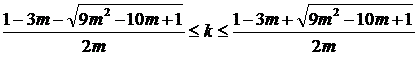 (8)
(8)