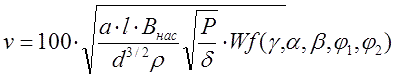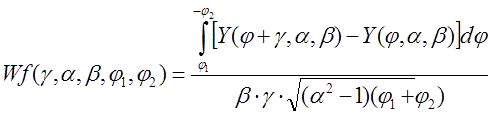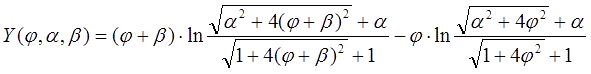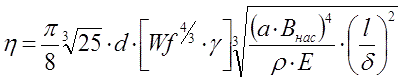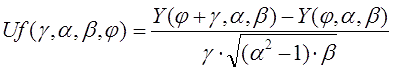| Главная » Статьи » Теоретические статьи » Математика coilgun |
В связи с тем, что падение форма Оружие будущего приобрело затяжной характер, я решил исправить некоторые ссылки в Таблице ускорителей. Кроме того, возникло желание сделать информацию в таблице более конкретной, а именно - учесть при расчете G-фактора такую величину, как длину снарядов. Поясню, с чем это связано.
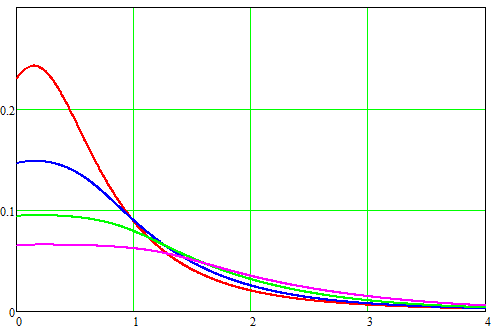
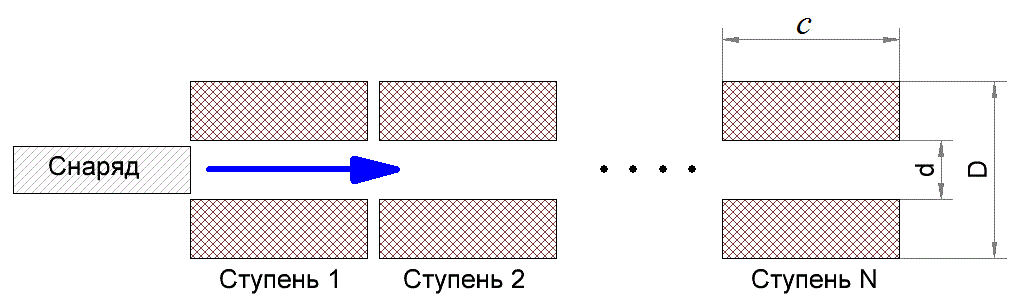
Как показано в данной публикации, значение выходной скорости сильно зависит от длины ускоряемого тела, а именно - растет с ее уменьшением (см. рис. 1). В результате койлганы, использующие короткие снаряды (а таких в таблице уже много - взять например шарометы Мегавольта), получают заведомо больший коэффициент качества G, чем неплохие ускорители, стреляющие "традиционными" цилиндрами. Такая ситуация неизбежна и обусловлена желанием применить для характеризации гауссовок их выходную скорость, не обращая внимания на КПД и прочие параметры. Однако, по здравом разумении, подобный подход нельзя считать полностью правильным. Действительно, поражающее действие снаряда в реальной жизни обусловлено все-таки его кинетической энергией. Скорость, которой уделено исключительное внимание при определении G-фактора, служит лишь для доставки снаряда к мишени по максимально настильной траектории, обеспечивающей необходимую точность стрельбы. Таким образом, для полной характеризации того или иного ускорителя, необходимо, вообще говоря, учитывать и форму снаряда, поскольку при сохранении калибра удлиннение метаемого тела повышает его кинетическую энергию (недаром в свое время огнестрельное оружие перешло от сферических снарядов к продолговатым). К счастью, полученные мной формулы позволяют это сделать. Для начала, надо их вспомнить. Так, для многоступенчатого койлгана длиной l, в котором катушки активируются по очереди, скорость снаряда имеет вид:
где геометрический множитель
а функция Y является безразмерным выражением форм-фактора катушки :
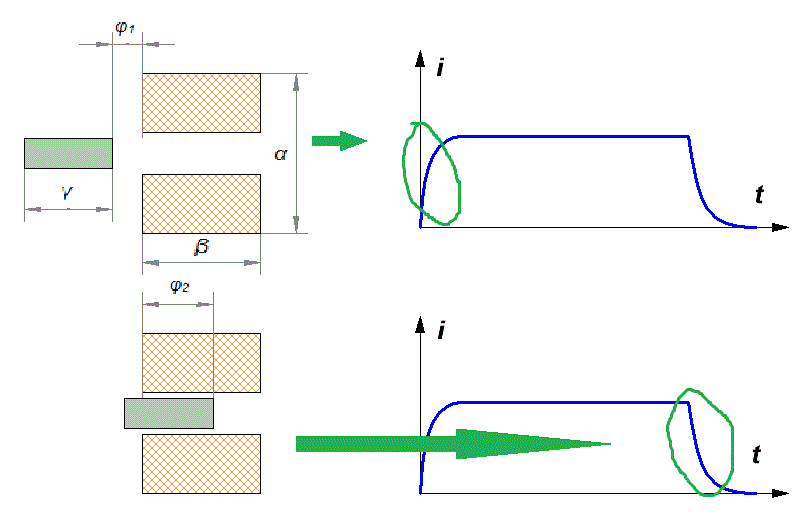
Напомню, что здесь все геометрические параметры переведены в безразмерный вид и выражены через калибр ускорителя d : D = α·d, c = β·d, длина снаряда z = γ·d, x1 = φ1·d, x2 = - φ2·d (см. рис. 2).
Рис. 2. Схема обозначений геометрических параметров. Другие входящие в формулу (1) параметры такие: a - безразмерное отношение калибра обмоточного провода "по меди" к его эффективному диаметру в изоляции (обычно получается a= 0,75..0,85) Внас - индукция насыщения материала снаряда, Тл δ - удельное сопротивление проводника обмотки, Ом·мм2/м E - затрачиваемая на выстрел электрическая энергия, Дж ρ - плотность материала снаряда, кг/м3 d - калибр койлгана - внутренний диаметр катушек, см l - суммарная длина ускоряющих катушек, см.
Для КПД в этой системе мной было получено такое соотношение:
В системе "бегущая волна", которая предусматривает возможность одновременного включения нескольких катушек, я получил аналогичную оценку для скорости и КПД, только с заменой в формулах (1) и (4) геометрического множителя Wf на множитель
где φ - координата виртуальной катушки, полученной включением нескольких обмоток (предполагается постоянной по длине ускорения). Фиксируя в соотношениях (2) и (5) параметр γ, можно получить оценки скорости и КПД для систем с конкретной длиной снаряда. Начав эту процедуру для нескольких койлганов из Таблицы, я с удивлением обнаружил, что предельное значение Wfmax ≈ 0.267, заявленное мной ранее, не соответствует действительности - в некоторых случаях я наткнулся на комбинацию параметров, которые давали большую величину! Например, Wf(0.1, 1.8, 0.1, 0.9, -0.2) = 0,269. После тщательного анализа ситуации я пришел к выводу, что ошибка была вызвана используемой итеративной процедурой нахождения максимума функции Wf - в зависимости от начальных условий и точности моделирования, она могла найти локальный , а не абсолютный максимум. Потратив еще немного времени, я обнаружил замечательную функцию Maximize, которая как нельзя лучше подошла для нашего случая. Эта операция (в теории) автоматически определяет абсолютный максимум функции нескольких переменных - достаточно лишь задать их диапазон, в котором происходит поиск. Правда, в действительности для надежной ее работы требуются некоторые "танцы с бубнами", но здесь я на этом останавливаться не буду. После использования Maximize выяснились довольно поразительные вещи. Во-первых, оказалось, что максимальное значение форм-фактора Wf достигается при нулевой длине снаряда и нулевой длине катушки (если про снаряд в принципе я догадывался - ранее установленное значение γ = 0.017 сразу показалось весьма "подозрительным" - то про катушку был, конечно, сюрприз). Во-вторых, максимум КПД для системы с изолированными обмотками также имеет место для бесконечно тонкой катушки (но, естественно, в случае снаряда конечной длины). Что касается системы "бегущая волна", то пересчет для нее дал еще более любопытный результат. Выяснилось, что предельно достижимая скорость в ней, а также максимальный КПД в точности равны таковым для койлгана с отдельно активируемыми обмотками. Более того, длина и диаметр обмоток в системах, соответствующие этим случаям, также совпадали! Разница была только в длине катушки (для случая "бегущей волны" она имеет ненулевое значение) и наборе оптимальных координат активации. Сводные результаты всех этих калькуляций сведены в Таблице 1. Таблица 1. Оптимальные параметры систем с отдельными катушками и "бегущей волной" для получения максимальной скорости и КПД ускорения.
Интерпретировать эти данные довольно затруднительно. Если получение максимума скорости для бесконечно тонкого снаряда вполне логично, то нулевая длина обмотки для койлгана с раздельной активацией, честно говоря, ставит меня в тупик. Совпадение геометрий для двух систем тоже пока выглядит необъяснимым. Возможно, эти две разновидности, на которые я условно разделил гауссовки, не так уж далеки друг от друга принципиально - ведь в реальных конструкциях активация соседних катушек вполне может осуществляться с некоторым "перекрытием" (то есть существует диапазон координат снаряда, где они работают одновременно). Или же здесь сказывается использованная в моих моделях идеализация формы тока в катушках в виде прямоугольных импульсов - учет времен нарастания и спада, возможно, привел бы к изменению всей картины... В любом случае, тут еще есть над чем поразмышлять... Последней корректировкой, которую я ввел в расчеты, было уточнение формулы для расчета КПД - ранее (см. например (4)) она определялась исходя из упрощенного соотношения
где Ekin - кинетическая энергия снаряда, Eel - затраченная электрическая энергия. Сие верно только для очень малых значений КПД (где Ekin << Eel). Более точная формула выглядит следующим образом:
Исходя из всех этих вводных, я провел корректировки моих статей и пересчитал цифры для примера реальной гауссовки, который в них приводится.
Теперь можно было приступить к коррекции собственно Таблицы, что я и сделал с учетом следующих моментов: 1) Расчет фактора G велся относительно значений скорости и КПД, достижимых в системе "бегущая волна" - это справедливо, т.к. такая система дает максимально возможные показатели. Сравнивать же реальные гауссовки со "сферическим конем в вакууме" (гипотетической конструкцией с нулевой длиной катушки) было бы странно. 2) В формулах учитывалась фиксированная длина снаряда по данным авторов соответствующих койлганов. К сожалению, эта информация для пары моделей оказалась недоступной, в связи с чем эти изделия в новую Таблицу не попали. Поэтому, на всякий случай, я сохранил старую версию таблицы, которая открывается по ссылке с основной страницы.
Как видно, в результате всех переделок, вид Таблицы существенно преобразился - койлганы немного "подровнялись" по качеству, и системы с короткими снарядами потеряли свое однозначное преимущество. Однако, две "рекордные" позиции, использующие транзисторный привод и рекуперацию - TK-14 и DB-6L сохранили свое лидирующее положение, что косвенно свидетельствует о правильности предложенной методики.
Всем успехов в творчестве,
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 125 | | | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |