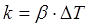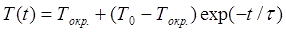| Главная » Статьи » Эксперименты » Прочие |
Вступление.
В своих недавних расчетах, посвященных исследованию факторов, ограничивающих скорость снаряда в ускорителях различных конструкций, я пришел к выводу, что доминирующим из этих факторов, особенно для малокалиберных койлганов, является омический нагрев ускоряющих обмоток. Пока энергоемкость портативных гауссовок была небольшой, эта проблема не выходила на первый план, но в последнее время с появлением мощных и скорострельных ускорителей она становится актуальной. В этой публикации описан эксперимент, который я поставил с целью определения тепловых свойств катушек, а именно - для изучения динамики их нагрева и остывания в различных условиях, характерных для для типовых портативных койлганов.
Задача и описание эксперимента. Для эксперимента я изготовил 4 катушки, фото и параметры которых приведены на рис. 1.
Рис. 1. Катушки, использованные для проведения эксперимента (слева) и их параметры (справа).
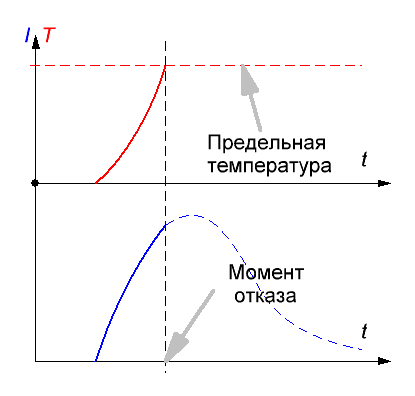
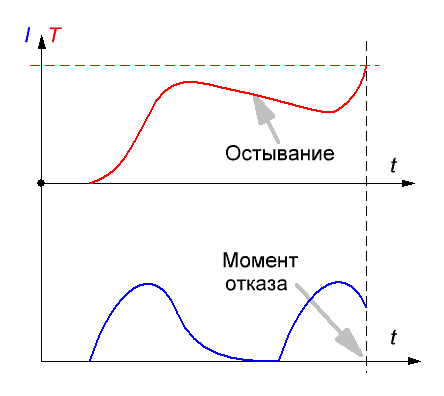
Для понимания того, почему были выбраны именно такие образцы, представим себе сначала, как происходит тепловыделение в обмотке гаусса при пропускании импульсного тока большой силы. Поскольку сам по себе процесс выстрела очень короткий (порядка и менее миллисекунды), то можно считать, что теплообмена с окружающей средой за это время нет и все омическое тепло целиком остается в катушке (такие процессы в физике называются адиабатическими). Если выделенная энергия превосходит некоторый предел, определяемый теплоемкостью обмотки, то происходит плавление проводника и разрушение катушки, либо повреждение изоляции между витками, что тоже эквивалентно отказу. Именно такой подход позволил мне в вышеприведенных публикациях оценить предельную энергоемкость катушек различной конфигурации (а значит, и накопительных конденсаторов) для случая одиночного выстрела. Очевидно, что условно "толстые" катушки будут иметь большую энергоемкость, чем "тонкие" такого же калибра и длины, поскольку имеют большую массу меди. Далее, если омическое тепло, выделяемое в катушке, не приводит к ее повреждению, то после фазы тепловыделения начинается процесс остывания, т. е. отдачи накопленного тепла в окружающую среду. Но если следующий выстрел происходит до того момента, как обмотка остыла, то порог энерговыделения может быть превышен, даже если во время предыдущего импульса этого не произошло. Такая ситуация, очевидно, как раз может иметь место в скорострельных койлганах, энергия одиночного выстрела в которых может быть небольшой.
Рис. 2. Иллюстрация условий перегрева катушки при одиночном (слева) и многократном (справа) импульсах тока.
Эти несложные рассуждения показывают, что для построения мощных и/или скорострельных систем критически важно знать такой параметр, как скорость теплообмена с окружающей средой. Обозначим эту величину k. Ее размерность, очевидно, равна Дж/сек. Ясно, что скорость остывания обмотки будет определяться каким-то соотношением k и массы, а точнее, теплоемкости С катушки. Попробуем понять, от чего может зависеть k для той или иной ситуации (той или иной катушки).
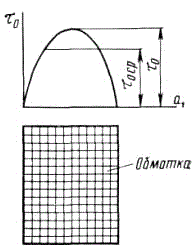
Во-первых, поскольку теплообмен происходит через наружную поверхность обмотки, то площадь этой поверхности S (т.е. габариты обмотки) должна влиять на процесс. Во-вторых, очевидно, будет зависимость от свойств внешней среды, для изучения чего была поставлена вторая часть эксперимента по исследованию параметров катушек, погруженных в эпоксидную смолу (эти условия соответствуют тем, в которых находятся обмотки в некоторых ускорителях моей конструкции, например ЕМ-3). В эту же категорию можно отнести и влияние скорости движения воздуха, охлаждающего обмотку – в специальной и справочной литературе можно найти множество данных на эту тему (зависимость допустимого тепловыделения различных приборов и поверхностей от скорости обдува и т.д.), но в данном случае я таких исследований не проводил (хотя сделать это было бы несложно). Наконец, интересно было бы изучить значение такого параметра, как толщина провода. В чем может быть его влияние? Представим, как происходит остывание обмотки. Ясно, что внешние ее слои должны остывать быстрее, т. к. находятся ближе к охлаждающей среде (то же самое можно сказать о внутренних слоях - для них возможна теплопередача через материал ствола или каркаса, на который намотана катушка). То есть, следует ожидать, что сформируется неравномерное поле температуры с максимумом где-то в глубине обмотки (см. рис. 3).
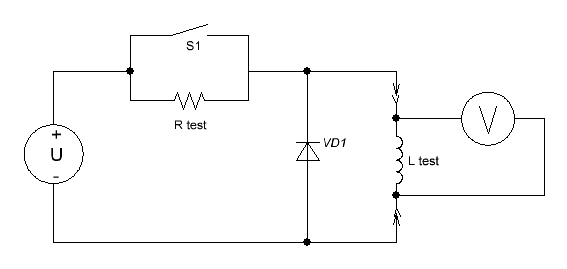
Тепло из этой глубины может передаваться двумя способами – вдоль провода (т.е. повторять путь электрического тока через витки обмотки), либо же напрямую через слои обмотки и разделяющую их электрическую изоляцию. Если первый механизм будет преобладать, то совершенно очевидно, что катушка, намотанная толстым проводом с небольшим количеством витков, будет остывать намного быстрее, чем идентичная по размерам катушка, содержащее большее количество витков тонкого провода. При этом следует ожидать, что скорость остывания будет подчиняться такой же зависимости от диаметра провода d, как и электрическое сопротивление R (поскольку теплопроводность материала, как и его электропроводность, пропорциональна площади сечения и обратно пропорциональна длине). В нашем случае, как легко можно показать, R ~ d - 4 , т. е. эта зависимость очень сильна. Если же будет преобладать «прямая» теплоотдача по кратчайшему пути, то такой зависимости мы не увидим (или она будет гораздо слабее). Скорость остывания здесь должна коррелировать скорее с площадью поверхности катушки, через которую происходит теплоотдача в окружающую среду. Исходя из приведенных соображении, для эксперимента были выбраны катушки двух различных диаметров – условно «тонкая» и «толстая», причем каждая в двух исполнениях – намоткой калибра Для нагрева катушек использовалось кратковременное (на 3…6 сек) их подключение к источникам тока большой мощности с помощью обычного ручного тумблера. Температура обмоток контролировалась путем измерения их активного сопротивления по значению падения напряжения при пропускании небольшого (несколько десятков мА) тестового тока. Для подачи этого тока использовались обычные резисторы, номиналы которых были подобраны таким образом, чтобы необходимый ток обеспечивался при подключении к тому же «разогревающему» источнику параллельно разомкнутому тумблеру. Наконец, для блокирования импульса самоиндукции при отключении тока разогрева в составе экспериментальной оснастки был предусмотрен обратносмещенный диод, включаемый параллельно исследуемой катушке (см. рис. 4). Внешний вид рабочего места показан на рис. 5, а типовая форма сигнала, записанного в одном из экспериментов (падения напряжения на катушке) – на рис. 6.
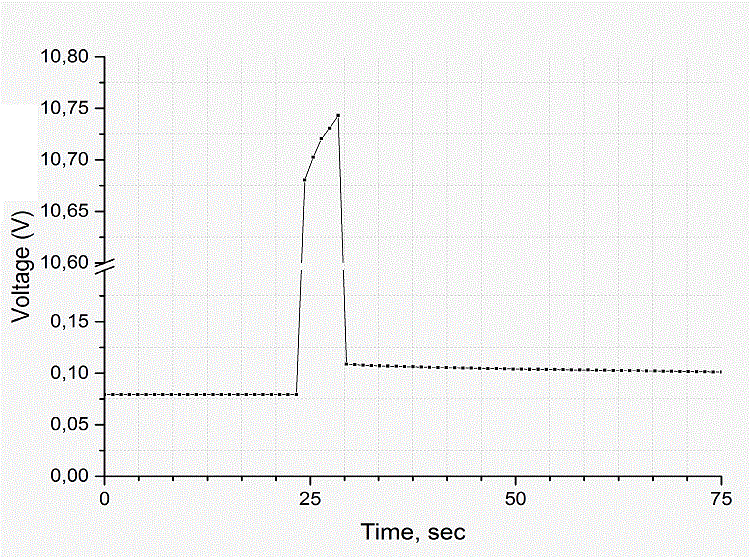
Рис. 6. Вид экспериментального сигнала.
Что мы видим на графике рис. 6 ? До включения тумблера сигнал постоянен и равен U = I·R, где I – тестовый ток, R – сопротивление обмотки при комнатной температуре. После кратковременной подачи греющего напряжения, тумблер вновь выключается, и катушка начинает остывать, при этом падение напряжения на ней можно представить как I·(1 + α·∆T)·R, где ∆T - разница между текущей температурой катушки и первоначальной (комнатной), а α – температурный коэффициент сопротивления меди, который хорошо известен и равен 0,0043 1/°С. Из приведенных соотношений можно оценить мгновенную температуру катушки, а из формы сигнала – определить величину скорости остывания k, о которой шла речь выше. Примечание: здесь надо оговориться, что под температурой Т (и сопротивлением R) здесь будет подразумеваться некое "среднеинтегральное" значение по обмотке, которое "видит" источник питания (реальное распределение температуры по сечению обмотки может быть довольно неравномерно, см. выше).
Результаты эксперимента и их обработка. В результате измерений были получены графики, подобные рис. 6, для каждого из образцов, сначала в "чистом" виде, потом для катушек, залитых эпоксидной смолой (см. рис. 7).
Далее планировалось получить значение k из уравнения для "классического" теплопереноса (закон Ньютона-Рихмана):
где ß - коэффициент пропорциональности (в общем случае, пропорциональный площади теплоотдачи S), ∆T - разница между температурой катушки и окружающей среды. Из этого закона, решив одно простое дифференциальное уравнение, легко получить формулу, описывающую мгновенную температуру остывающего тела:
Здесь Tокр. - температура окружающей среды (принимается равной комнатной), T0 - начальная температура катушки перед остыванием, τ - постоянная времени остывания. Причем можно показать, что τ = C/ß , а
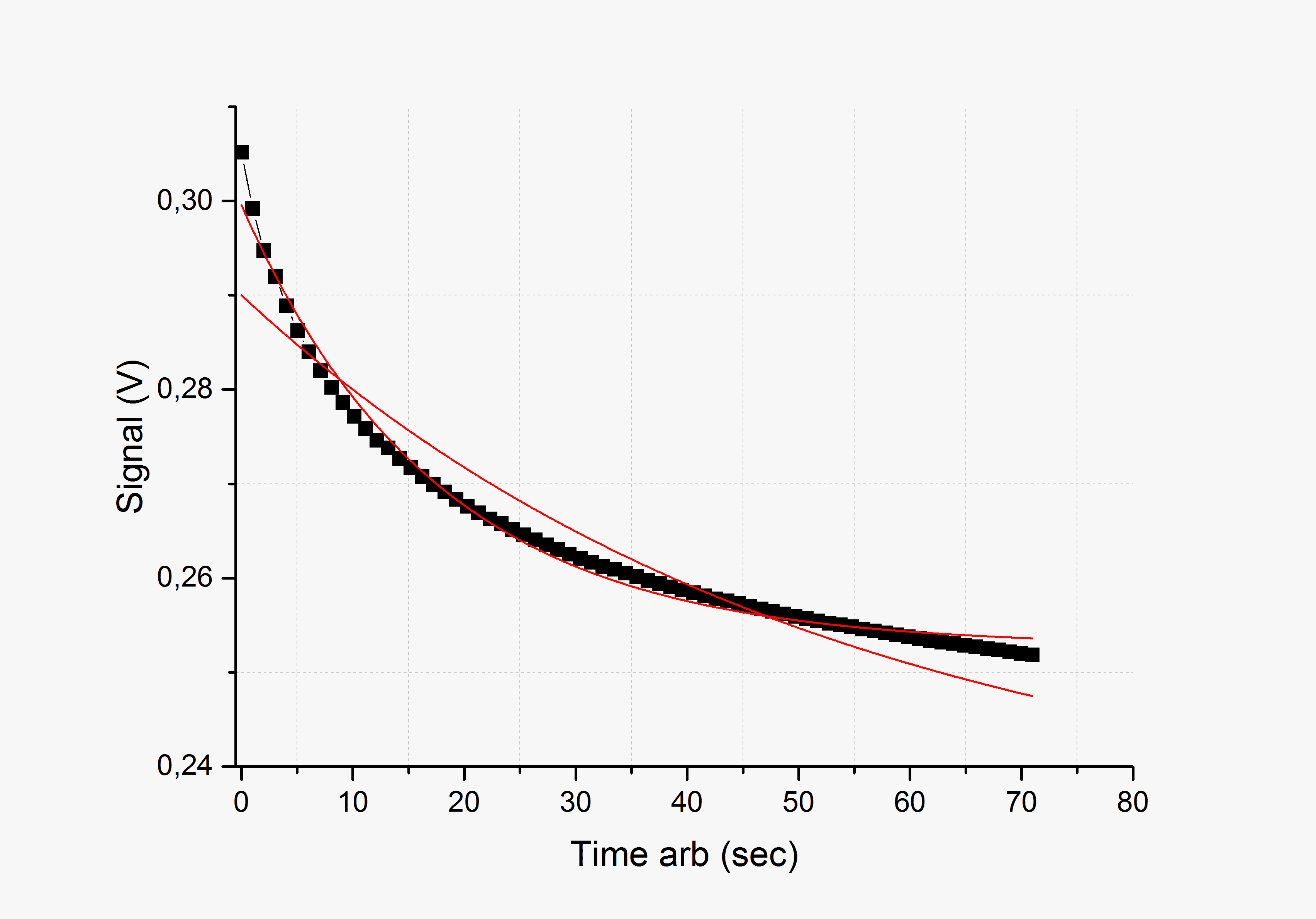
где dT/dt - производная во времени от температуры катушки (т. е. скорость остывания), а С, напомним - ее теплоемкость (она может быть легко вычислена через массу обмотки и удельную теплоемкость меди, которая хорошо известна). Согласно формуле (2), скорость остывания подчиняется экспоненциальному закону. Однако, при обработке экспериментальных данных выяснилось, что они довольно плохо следуют такому тренду (см. рис. 8). Причем наиболее сильные отклонения от экспоненты наблюдаются в окончательной стадии процесса (когда разница температур обмотки и окружающей среды снижается). То есть катушка остывает сначала быстро, затем скорость остывания резко уменьшается. Примечание: объяснения такого поведения существуют и кроются как раз в том, что начальное поле температуры в катушке сильно неоднородно, вследствие чего описание по ф-ле (1) является чересчур упрощенным. Точное тепловое поведение каждого сегмента обмотки может быть получено методом численного моделирования, и существуют симуляции подобного рода, проведенные специально для электромагнитных ускорителей (см. например H.Chen et al, "Temperature Distribution Analysis of a Switched Reluctance Linear Launcher", IEEE Trans. on Plasma Sci., Vol. 41, No. 5, May 2013). Мало того, оказывается, что попытка "свободной" (без ограничения значений параметров) аппроксимации полученных зависимостей приводит не только к искажению показателя экспоненты, но и конечного значения температуры, к которому стремятся графики (оно, вообще говоря, известно и равно просто комнатной температуре воздуха, т. е. около 25ºС).
Рис. 8. Значение тестового падения напряжения при постоянном токе на остывающей катушке (Signal) в зависимости от времени процесса (Time). Черные квадраты - экспериментальные точки, красные линии - попытки аппроксимации экспоненциальными кривыми с различными коэффициентами. Как видно, эти кривые весьма трудно применить ко всему набору точек.
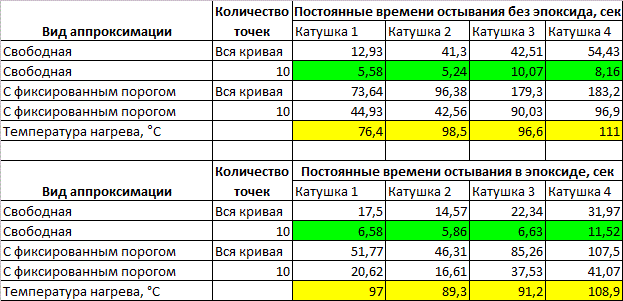
Поэтому каждая зависимость аппроксимировалась 4 раза - "свободным" способом (т. е. вся кривая "как есть"), с фиксированным порогом (т. е. конечная температура принудительно устанавливалась на уровне 25ºС), и то же самое только для первых 10 точек графика. Значение постоянной времени остывания, полученное для свободной аппроксимации начального участка зависимостей, выделено в Табл. 1 зеленым цветом, а табулированная по ф-ле (1) начальная величина температуры остывания T0 (она же пиковое значение температуры катушки в эксперименте, достигаемое непосредственно перед отключением силового тумблера S1) - желтым. Эти величины представляют интерес с точки зрения анализа наиболее критичных для катушки режимов ( см. ниже).
Таблица 1. Результаты эксперимента по исследованию динамики остывания катушек без эпоксидной заливки (верхняя таблица) и с заливкой (нижняя таблица).
Как видно, значения τ, полученные различными методами, отличаются очень сильно (более, чем на порядок величины). Поэтому вопрос о том, какое из них считать "истинным", довольно сложен. Вообще-то, достигаемая в эксперименте температура нагрева хоть и существенная, но далеко не достаточная для повреждения эмалевой изоляции провода (для этого надо где-то 300 ºС), и тем более для его расплавления. То есть реальные отказы будут происходить при более сильном нагреве. Но при приближении к таким температурам скорость остывания также будет существенно выше, чем измеренная на опыте, а значения τ - гораздо меньше приведенных в таблице 1 из-за упомянутого отклонения полученных зависимостей от чисто "экспоненциального" вида. То есть, хоть остывание в целом будет происходить довольно медленно (см. рис. 6), но уход из зоны "опасных" для обмотки температур будет очень быстрым. В такой ситуации для оценки "живучести" катушки целесообразно взять минимальные измеренные в эксперименте значения τ (а это и есть закрашенные зеленым ячейки табл. 1). Для изучения механизма теплоотдачи в окружающую среду для каждой катушки были вычислены усредненные значения τ и построены на одном графике вместе со значениями электрических сопротивлений, и величиной, равной отношению теплоемкости и площади поверхности каждой из катушек (согласно пояснению к ф-ле (2), результат такого действия должен хорошо коррелировать с постоянной остывания). То, что получилось, изображено на рис. 9. Для удобства все величины нормализованы, т. е. поделены на соответствующие значения для первой катушки.
Рис. 9. Нормализованные величины τ, R и С/S для исследованных катушек.
Как видно, значения постоянной времени остывания, как и предсказывает классическая теория, гораздо лучше соотносятся с величинами C/S, чем с R. Отсюда можно заключить, что доминирующим механизмом теплопередачи из глубины обмотки в окружающую среду является тепловой поток "через слои" к наружной поверхности катушки, а не "вдоль провода". Наконец, исходя из соотношения (3), для каждой из обмоток была оценена величина скорости теплообмена с окружающей средой k для максимальной температуры, достигнутой в эксперименте (т. е. в самом начале процесса остывания). Эти значения приведены в табл. 2.
Таблица 2. Скорость теплоообмена при остывании исследованных катушек (без эпоксидной заливки).
Видно, что интенсивность теплообмена для исследованных образцов находится в диапазоне 4...20 Дж/сек. Опираясь на эти величины, можно оценить допустимую скорострельность того или иного койлгана при условии, что известны затраты энергии для каждой из его ступеней. Например, для Электрического лука ЕМ-3, ступени которого по параметрам близки к катушкам № 3 и 4, исходя из энергоемкости его конденсаторов, получается, что при сохранении температуры катушек около 100 ºС можно делать один выстрел каждые 7 секунд.
Выводы. 1) Постоянные времени остывания всех исследованных катушек в области максимальных температур лежат в диапазоне 5..12 сек. Поскольку за время ≈ 3τ катушка остывает довольно сильно, то можно утверждать, что для мощных койлганов калибра около 7 мм, работающих на пределе температурного ограничения (т. е. при каждом выстреле которых катушки разогреваются почти до предельно допустимой температуры), длительность перезарядки конденсаторной батареи нецелесообразно делать менее 30 секунд. 2) "Тонкие" катушки остывают, как и ожидалось, быстрее, чем "толстые", но скорость остывания не пропорциональна теплоемкости (массе) катушек. Напротив, корреляция постоянной остывания с величиной, равной отношению теплоемкости катушки и площади ее поверхности, довольно хорошая. В целом можно сказать, что "толстые" катушки остывают приблизительно вдвое медленнее, чем "тонкие". 3) Влияние калибра провода на скорость остывания оказалось незначительным. В сочетании с предыдущим пунктом это говорит о том, что доминирующим механизмом теплопередачи из глубины обмотки в окружающую среду является тепловой поток "через слои" к наружной поверхности катушки, а не "вдоль провода". Следовательно, для создания скорострельных гауссовок или койлганов большой мощности можно смело выбирать диаметры провода, руководствуясь исключительно необходимыми электрическими параметрами системы (в противном случае, для ускорения остывания предпочтительно было бы использование низковольтных систем с проводниками большого сечения). 4) Скорость теплообмена с окружающей средой для исследованных образцов катушек составляет 4...20 Дж/сек для температур обмотки в районе 100 ºС. Полученные данные позволяют оценить допустимую скорострельность того или иного койлгана при условии, что известны затраты энергии для каждой из его ступеней. 5) Заливка катушек эпоксидной смолой оказывает неоднозначный эффект на скорость остывания. При "свободной" аппроксимации начального участка кривой охлаждение в большинстве случаев слегка замедляется, но во всех остальных вариантах зависимость обратная. Однако, в любом случае, изменение интенсивности теплообмена при эпоксидной заливке не превышает 2 раз, т. е. не является радикальным.
Всем успехов в творчестве, Ваш Eugen.
| |||||||||||||||||||||||||||||
| Просмотров: 547 | | | |||||||||||||||||||||||||||||
| Всего комментариев: 0 | |