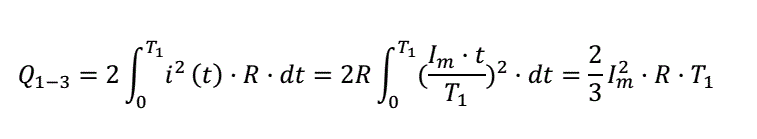| Главная » Статьи » Теоретические статьи » Математика coilgun |
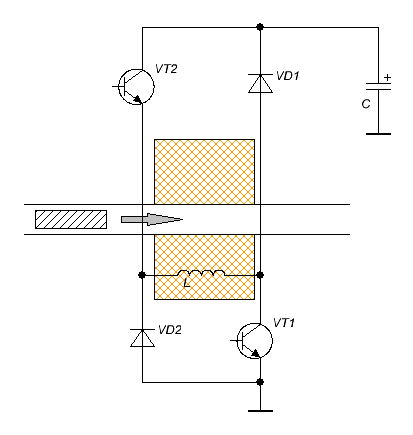
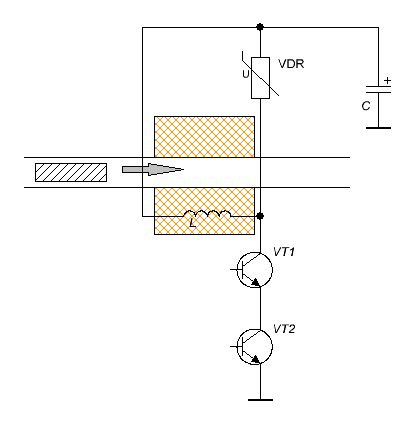
В статье "Исследование эффективности рекуперации энергии в схеме полумостового электромагнитного ускорителя" мной были рассчитаны зависимости КПД рекуперации койлгана по схеме "косого" полумоста от различных параметров, в том числе от начальной скорости снаряда. Там же было обещано проведение моделирования в пакете FEMM для оценки полного (с учетом рекуперации) КПД ускорения снаряда. В данной публикации приводятся результаты такого расчета, причем не только для полумостового гаусса, но и для более простой конфигурации с гасящим варистором, включенным параллельно ускоряющей катушке. Эти топологии изображены на рис. 1 (более полный перечень возможных схем построения койлганов с перечислением особенностей их функционирования, достоинств и недостатков приведен мной здесь).
В качестве изначальных условий для моделирования были выбраны следующие: скорость снаряда 80 м/с, емкость конденсатора 5000 мкФ, начальное напряжение 400 В. То есть имелся в виду достаточно мощный ускоритель, у которого в начале процесса выстрела напряжение составляло, к примеру 450 В (это соответствует суммарной энергоемкости 4502*5000/2 000 000 ≈ 506 Дж, что, вероятно, близко к предельным массогабаритам для портативного койлгана и соответствует, например, 5 конденсаторам 450Вх1000 мкФ), а к рассматриваемому моменту снизилось до 400 В. Если считать что на выстрел расходуется половина заложенной в емкости энергии, то конечное напряжение на выходе из ствола ускорителя может составить 318 В. Иными словами, моделируется одна из ступеней, расположенных где-то в середине ствола многоступенчатой гауссовки ( с конечной скоростью снаряда, вероятно, более 120 м/с). Геометрия системы была выбрана следующая: длина катушки и снаряда 16 мм, внутренний диаметр катушки 8 мм, калибр цилиндрического снаряда - 6 мм. При этом моделирование проводилось в диапазоне наружных диаметров катушки (и, соответственно, диаметра провода) вплоть до 24 мм, т. е. "толстой" катушки по классификации этой статьи. Там же показано, что КПД рекуперации энергии для подобных геометрий катушек и скоростей снарядов выходит на насыщение и достигает значений порядка 80 %. То есть, логично было бы ожидать получение очень высокого суммарного КПД ускорения снаряда. Дополнительным ограничением служила максимальная сила тока в ключах - 200 А. Таким образом, для обеих схем на рис. 1 были использованы ключи с максимальным напряжением 450 В и током 200 А - это приблизительно соответствует параметрам мощных кремниевых IGBT-транзисторов, имеющихся в продаже на сегодняшний день. При этом для полумостовой схемы силовые диоды VD1, VD2 должны выдерживать обратное напряжение емкости (450 В), как и варистор VDR1 на рис. 1 (б). То есть, стоимость силовых компонентов для обеих схем приблизительно одинакова. Со схемотехникой все сложнее - если в топологии с гасящим варистором два последовательно соединенных ключа в реальной схеме можно (и нужно) заменить одним более мощным транзистором с удвоенным напряжением, то в полумосте такой возможности нет, причем для каждого ключа надо делать отдельную драйверную схему с плавающим питанием, как это сделано, например, здесь. В обоих случаях к катушке прикладывается одинаковое обратное напряжение - 400 В, что должно обеспечить идентичную скорость спада тока для одинаковых (т.е. имеющих схожую индуктивность) катушек. Все прочие подробности расчетов (включая использованные для этого скрипты) приведены на этой страничке. Перед тем, как перейти к анализу результатов, необходимо сделать одно важное замечание. Дело в том, что весь анализ, сделанный в "Исследовании эффективности рекуперации энергии в схеме полумостового электромагнитного ускорителя", касался того случая, когда импульс тока в катушке имеет близкую к треугольной форму - ключи открываются, ток нарастает до некоторого максимального значения, затем оба ключа одновременно закрываются и ток спадает до нуля, "закачивая" заряд обратно в конденсатор. Но в практически реализованных конструкциях (см. например тот же койлган Dantist'a) между этими двумя циклами имеет место промежуток времени, в течение которого открыт только один ключ, и ток свободно циркулирует в катушке, постепенно затухая за счет ее активного сопротивления, либо же второй ключ периодически приоткрывается, удерживая значение тока вблизи заданного значения (т. е. используется стабилизация тока).
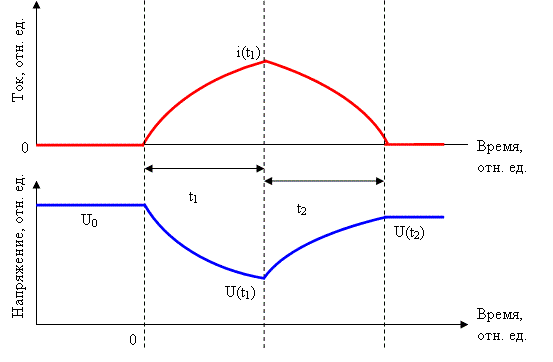
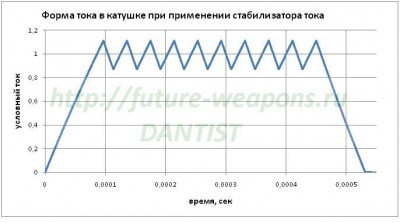
Рис. 2. Теоретические формы тока и напряжения в полумостовой схеме при непосредственном следовании цикла рекуперации за циклом накопления (слева), и ток в катушке для реальной конструкции полумостового койлганам (справа).
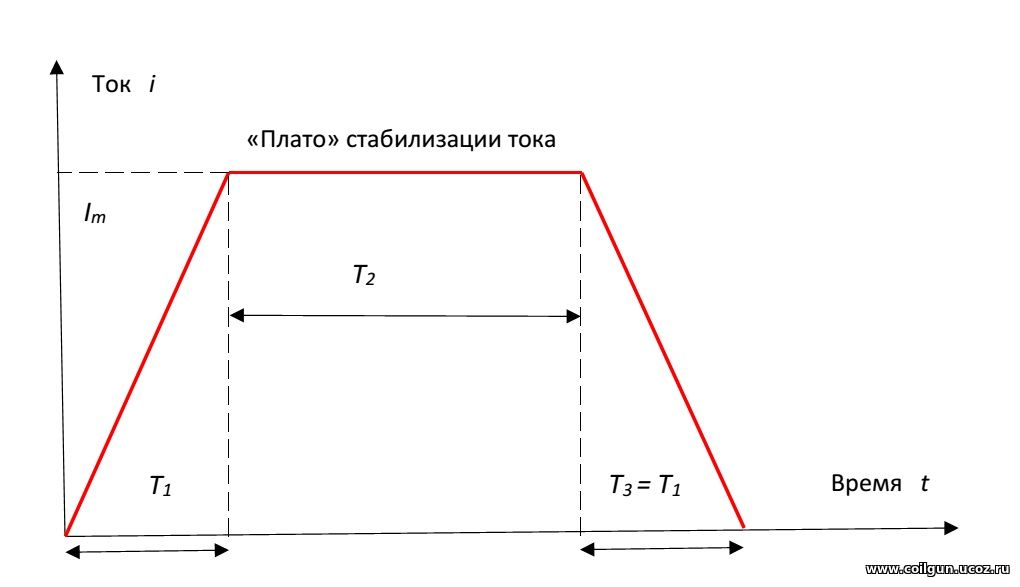
Более подробно функционирование подобной схемы разъясняется автором там же, здесь мы только отметим, что ее применение обусловлено желанием использовать одинаковые катушки на всех ступенях ускорения. В результате, на первых ступенях (когда скорость снаряда еще мала), ток необходимо ограничивать, чтобы он не превысил максимально допустимое для ключей значение, что и достигается закрытием одного из ключей. По мере ускорения снаряда и сокращения суммарной длительности токового импульса в каждой ступени, отрезок времени, в течение которого ток циркулирует вблизи уровня ограничения, сокращается, и для последней катушки ток может принять "идеальную" форму как на рис. 2 слева (то есть, остаются только фронты нарастания и спада тока, соответствующие циклам накопления и рекуперации). Но для всех катушек, кроме последней, на осциллограмме тока будет присутствовать "плато". Это обстоятельство кардинально меняет ситуацию, поскольку на протяжении промежуточного цикла циркуляции тока никакой рекуперации не происходит, в то же время в систему вносятся дополнительные омические потери энергии. Попробуем их оценить, не переходя к сложным вычислениям. Для этого предположим, что фронты нарастания и спада тока одинаковы и строго линейны, а ток на "плато" имеет постоянное значение Im (это можно устроить, если в схеме стабилизации, примененной Dantist'ом, использовать следящий компаратор с очень малым гистерезисом). Длительность фронтов обозначим как T1, длительность "плато" - T2, активное сопротивление катушки - R.
Рис. 3. Иллюстрация к упрощенной модели расчета потерь на этапе стабилизации тока.
Тогда суммарные омические потери на фронтах составят
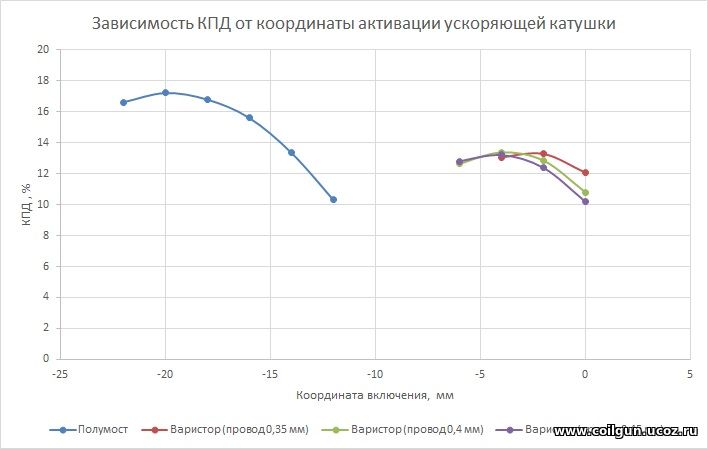
а на "плато" просто Q2 = Im2 ·R ·T2. Таким образом, Q2 = Q1-3·1,5·T2/T1. Легко видеть, что даже при небольшом "плато" омические потери существенно нарастают (и. следовательно, падает КПД рекуперации). Так, при Т2 = 2/3·Т1 Q2 = Q1-3 (т. е. потери энергии удваиваются), а при длительности "плато", равной суммарной длительности фронтов (Т2 = 2Т1) Q2 = 3Q1-3. В последнем случае, исходное (без участка стабилизации) КПД рекуперации схемы 80% после введения интервала свободной циркуляции тока превратится в 40%, а исходное значение 70% упадет до 10% ! Получается, что введение цикла свободной циркуляции тока может "съесть" почти весь выигрыш от рекуперации энергии. Выходом из ситуации могло бы стать использование на каждой ступени катушки, подобранной по габаритам под соответствующую скорость снаряда таким образом, чтобы спад тока следовал сразу после нарастания. К сожалению, это предложение чисто гипотетическое, поскольку в реальной конструкции все параметры (в том числе индуктивность наматываемой катушки, а также ожидаемая скорость снаряда и напряжение на емкости в момент активации определенной ступени) могут быть оценены с определенной погрешностью, иногда довольно существенной. Поэтому, во избежание превышения допустимых режимов силовых ключей, в схему все равно придется вводить принудительное ограничение тока, которое неизбежно будет срабатывать (в противном случае, если ток не достигает максимального значения, ключи будут использоваться неэффективно). Резюмируя эти соображения, можно утверждать, что КПД рекуперации энергии в реальных конструкциях полумостовых койлганов, особенно с одинаковыми ускоряющими ступенями, будет существенно уступать теоретически рассчитанным здесь значениям. Теперь вернемся к нашим расчетам и посмотрим, что получается для "идеального" случая, когда стабилизация тока отсутствует и цикл рекуперации наступает сразу после фронта нарастания тока. На рис. 4. продемонстрировано КПД для полумостовой системы и системы с варистором, причем для полумоста рассматривалась только "толстая" катушка с диаметром 24 мм (для нее эффективность рекуперации выше, для "тонкой"), а для варистора - набор диаметров, соответствующих разным калибрам провода (0,35 , 0,4 , и 0,45 мм). Для корректного сравнения выбирались условия, при которых энергия, затрачиваемая на выстрел, в обеих системах была одинакова (около 7,5 Дж). Поскольку диаметр катушки для полумоста был фиксированный, то диаметр провода, соответствующий всем приведенным выше условиям, здесь оказался единственный - 0,6 мм. В результате, варьируемым параметром моделирования выступила координата активации, т. е. расстояние от носа снаряда до переднего торца катушки, при котором происходит открытие ключей.
Рис. 4.
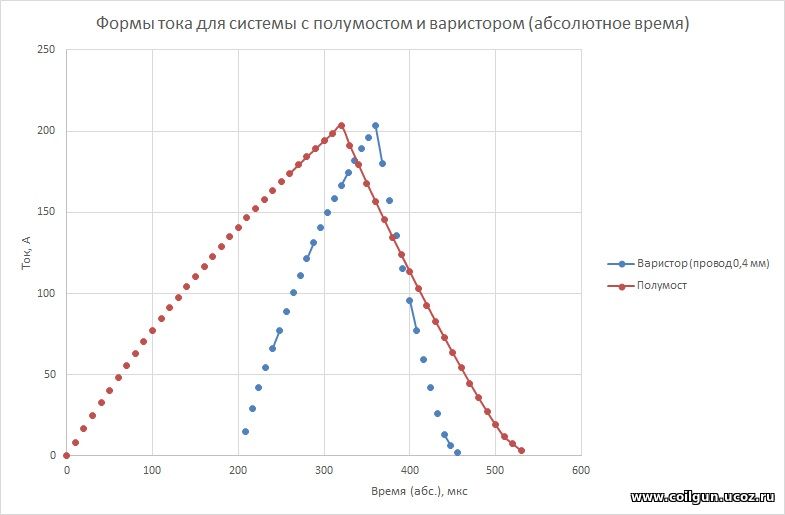
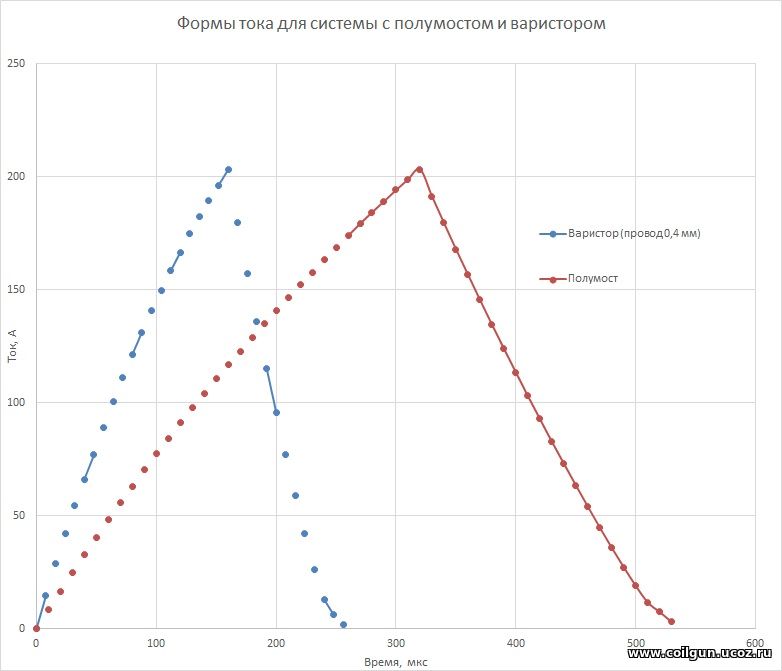
Из графика видны два существенных момента: во-первых, КПД рекуперационной схемы выше, но незначительно (ок 17 % против 13,5 % для варисторной конфигурации), во-вторых, оптимальная координата активации для толстой катушки расположена дальше, чем для для тонкой. Второе обстоятельство легко объяснимо, если принять во внимание, что радиус действия магнитного поля тем больше, чем выше наружный диаметр обмотки. Кроме того, спад тока для более толстой катушки будет длиннее (т. к. больше ее индуктивность), поэтому, для сохранения КПД и фиксированной затрачиваемой энергии, ее необходимо как активировать, так и выключать раньше, чем "тонкий" аналог. В подтверждение этого тезиса на рис. 5 изображены формы тока для этих двух случаев (для варистора рассмотрен только случай провода 0,4 мм, соответствующий максимуму КПД).
Рис. 5. Формы тока для варисторной и полумостовой схемы, отображенные на единой шкале времени с началом в точке активации катушки полумостовой конфигурации (сверху), а также взятые с одной точкой отсчета (снизу). Затем были рассмотрены варианты полумостовой системы с более тонкой катушкой (и, соответственно, другими диаметрами провода). Результат моделирования изображен на рис. 6 для случая провода калибром 0,5 мм.
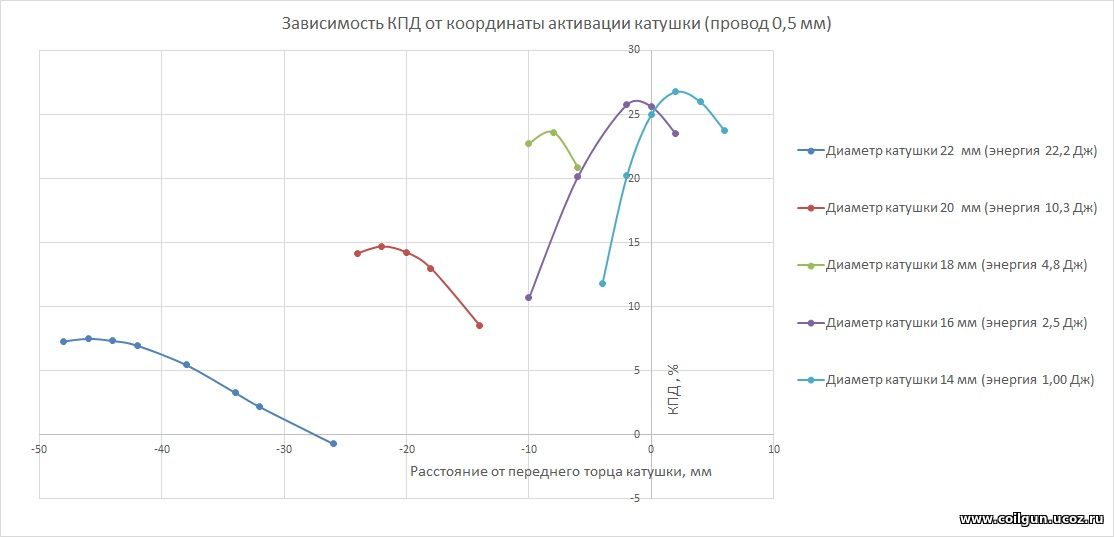
Рис. 6. Зависимость КПД от координаты активации в полумостовой системе с диаметром провода по меди 0,5 мм. Для каждого случая указана затрачиваемая на выстрел энергия.
Подобные зависимости для набора различных диаметров провода приведены здесь. На рис. 6 можно констатировать, что оптимальная координата активации катушки большого диаметра может лежать на значительных расстояниях, превышающих удвоенную длину катушки. Это говорит о необходимости использования каких-то алгоритмов обработки сигнала с датчиков, следящих за положением снаряда в стволе, т. к. активация ступени от датчиков, непосредственно к ней прилегающих, становится в этом случае невозможной. Попытка же включения катушки при подлете снаряда на более близкие к ней расстояния может привести к тому, что затянутый спад тока начинает тормозить снаряд, да так, что итоговое приращение скорости на выходе из ступени может стать отрицательным (этому соответствует участок отрицательного КПД при расстоянии активации менее 30 мм для катушки диаметром 22 мм). Кроме того, затягивание импульса в случае "толстых" катушек приводит к соответствующему росту затрачиваемой на выстрел энергии (это понятно, т. к. максимальный уровень тока, т. е. высота вершины "треугольника" на рис. 5, у нас всюду одинакова и составляет, как было условлено, около 200 А). Очень важным выводом, который также следует из рис. 6, является то, что уменьшение диаметра катушки (в сторону значений, оптимальных для "обычной" схемы с варистором), также приводит к росту КПД рекуперативной конфигурации (хотя сама по себе эффективность рекуперации при этом должна падать). Из этого ясно, что выигрыш от возвращения в конденсатор значительной части энергии для "толстых" катушек не компенсирует проигрыша в КПД ускорения снаряда, который возникает вследствие неоптимальности геометрии такой катушки (особенно на высоких скоростях снаряда). И это при том, что рекуперация при таких коротких импульсах уже способна вернуть до 80% затрачиваемой энергии ! Подобрав для каждого диаметра намоточного провода координату активации, соответствующую максимуму КПД, можно попробовать изобразить на одном графике (рис. 7) семейства кривых зависимости КПД от скорости снаряда на выходе из катушки (затрачиваемая на выстрел энергия при этом для каждого случая, конечно, разная). На этом же графике изображены данные для системы с варистором (соответствующие им зависимости от координаты показаны выше на рис. 4).
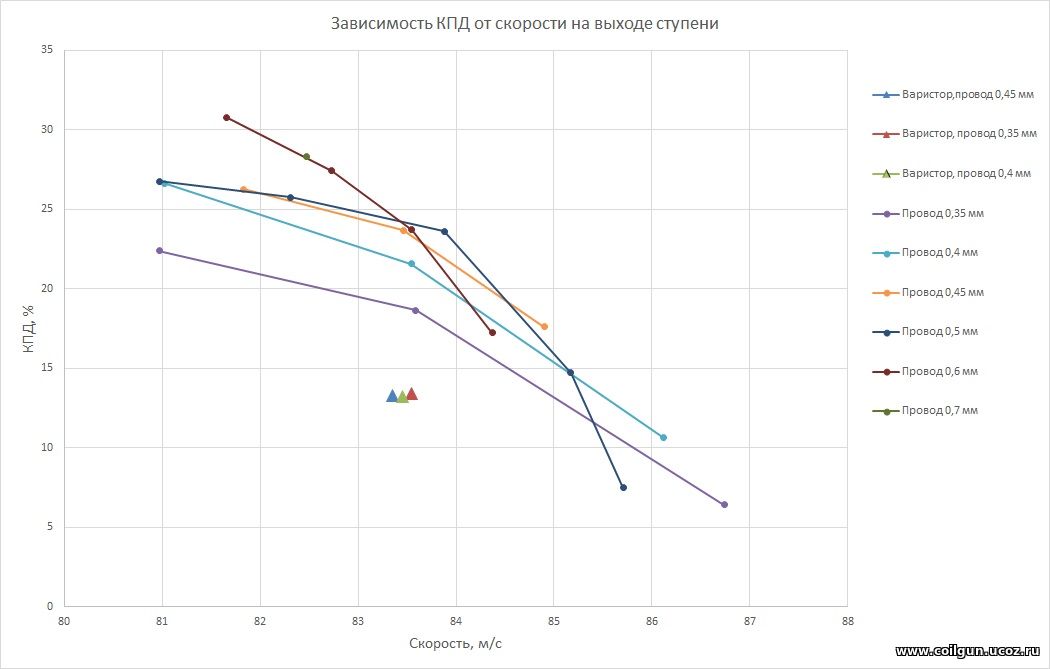
Рис. 7.
Видно, что полумостовая схема потенциально может обеспечить КПД ускорения более 30 %, но при этом само значение приобретаемой скорости становится незначительным. То есть мы имеем классическую для койлганов картину - снижение затрачиваемой на разгон энергии приводит к росту КПД, но снаряд приобретает меньшую скорость. Если бы речь шла о стационарной системе с неограниченной длиной ствола, то это не представляло бы проблемы - увеличивай количество ступеней сколько угодно, и получай сверхвысокоэффективное ускорение. Но так как мы рассматриваем портативный гаусс, то обязаны наложить некие ограничения на минимальную скорость (приращение скорости), которую должно приобретать метаемое тело в каждой катушке. Об этой проблеме и следствиях из нее я тоже подробно писал в этой статье, здесь же можно сделать следующую простую прикидку. Допустим, мы хотим получить скорость на выходе гауссовки 120 м/с на длине ускорения 0,6 м (что эквивалентно приблизительно 30 катушкам длиной 16 мм с учетом дополнительного места, необходимо для датчиков и прочих конструктивных элементов, располагаемых вдоль ствола койлгана). Тогда на каждой ступени снаряд должен приобретать не менее 4 м/с при условии, что рост скорости одинаков для всех ступеней (как продемонстрировано, например, здесь, это предположение правдоподобно для многоступенчатых систем). Если же считать, что движение близко к равноускоренному, то скорость снаряда пропорциональна корню квадратному из расстояния (номера ступени). Тогда ступень, соответствующая скорости 80 м/с (т.е. 2/3 от максимальной), должна находиться где-то на 4/9 длины ствола (т. е. практически в его середине) и приращение скорости должно быть ½ от максимального. Т. е. если считать, что на последней ступени снаряд приобретает дополнительную скорость 2,5 м/с, а на первой - 10 м/с, то приходим для какой-то "средней" ступени к похожей цифре 5 м/с. Все эти значения весьма правдоподобны, хоть и основаны на "волюнтаристских" предположениях.
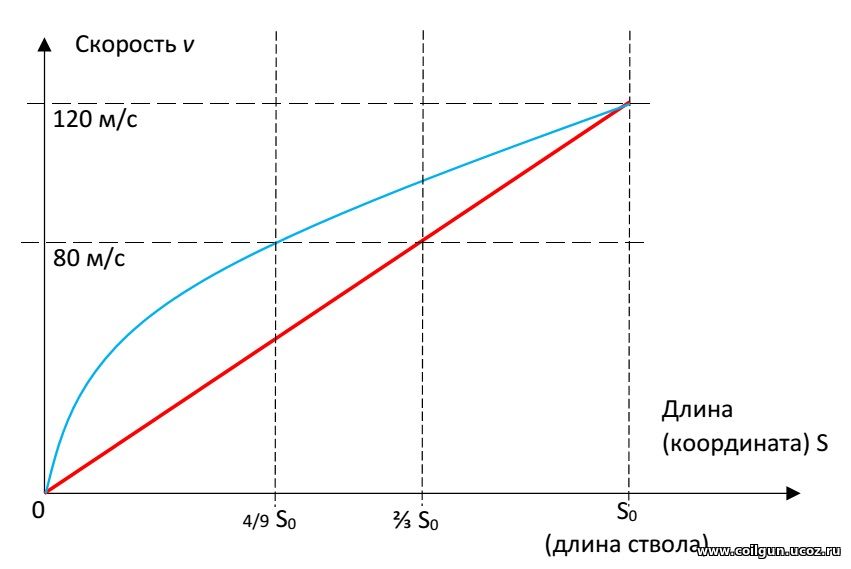
Рис. 8. Схема ускорения снаряда в койлгане - равноускоренная (голубой цвет) и с равным приращением скорости на всех ступенях (красный).
В реальности, вероятно, картина будет какая-то промежуточная между этими двумя случаями (т. е. ускорение снаряда будет происходить чуть медленнее, чем при равноускоренном движении, но быстрее, чем при линейном росте скорости от расстояния). В любом случае, приращение скорости в 1...2,5 м/с, соответствующее высоким КПД полумостовой схемы на рис. 7, является совершенно недостаточным для портативного ускорителя. Более реалистичные величины приращения в 3 и более м/с достигаются при КПД 25 % и меньше, т. е. дают менее чем двухкратный рост КПД по сравнению с "варисторной" схемой (при одинаковом приращении скорости). Кроме того, можно видеть, что полумост позволяет получить большее приращение скорости (приблизительно в 1,5 ..2 раз) при сохранении того же КПД, что и "варисторная" конфигурация. Правда, достигается это соответствующим ростом затрачиваемой на выстрел энергии (например, при диаметре катушки 20 мм, намотанной проводом 0,5 мм и затраченной энергии 10,3 Дж получаем для полумоста КПД 14,7 % при скорости 85,2 м/с, тогда как схема с варистором имеет близкой КПД при скорости 83,5 м/с и затрачиваемой энергии 7,6 Дж). Таким образом, можно заключить, что при эквивалентных характеристиках приращения скорости снаряда и энергозатратах, полумостовая схема обеспечивает КПД не более чем в 2 раза выше, чем традиционные конфигурации (например, схема с гасящим "варистором"). Причем это в оптимальных условиях, а именно - при отсутствии интервала "стабилизации" тока (т. е. когда каждая катушка подобрана под соответствующую скорость снаряда). Если же мы имеем многоступенчатую гауссовку, в которой все катушки одинаковые и оптимальные условия достигаются только на последней из них, то усредненный рост КПД составит, вероятно, не более 1,5 раз. Использовать этот выигрыш можно разными способами, самый разумный из которых, на мой взгляд - сокращение емкости запасающего конденсатора. Это позволит уменьшить массогабариты гауссовки и повысить ее скорострельность, поскольку, при сохранении мощности преобразователя напряжения, уменьшение заряжаемой емкости приводит к ускорению ее перезарядки до необходимого напряжения после каждого выстрела. Является ли повышение сложности конструкции и удорожание электронной части койлгана, связанное с использованием полумоста, разумной платой за получение таких "бонусов" - решать каждому конструктору самостоятельно.
В заключение попробуем формулировать основные выводы из проведенного исследования:
1) Для максимальной реализации возможности рекуперации энергии, заложенной в конфигурации "косого" полумоста, необходимо подбирать геометрические характеристики катушки таким образом, чтобы форма тока была близка к треугольной и "плато", соответствующее состоянию системы с одним открытым ключом, было как можно более коротким. Из этого вытекает необходимость использования различных катушек в каждой ступени многоступенчатого ускорителя. Использование же одинаковых катушек в этом случае резко снижает возможный КПД. 2) При выборе геометрии катушки следует скорее увеличивать КПД ускорения снаряда, а не КПД рекуперации - это приводит к росту суммарной эффективности системы. То есть "толстые" катушки, несмотря на повышенную способность к возврату энергии в емкость, не являются в полумостовой схеме оптимальными (по-крайней мере, в районе скоростей снаряда около 100 м/с). 3) Для выбранных характеристик системы использование полумоста позволяет повысить суммарный КПД многоступенчатого ускорителя, вероятно, не более чем в 1,5 раз по сравнению с традиционными схемами без возврата части энергии в конденсатор (например, схемы с гасящим варистором). Это повышение выражается в уменьшении суммарной энергии, затрачиваемой на каждой ступени (а не в росте скорости снаряда), и может быть использовано для соответствующего снижения емкости запасающего конденсатора.
Всем успехов в творчестве, Eugen | |||||||||
| Просмотров: 1738 | | |||||||||
| Всего комментариев: 0 | |