| Главная » Статьи » Теоретические статьи » Математика coilgun |
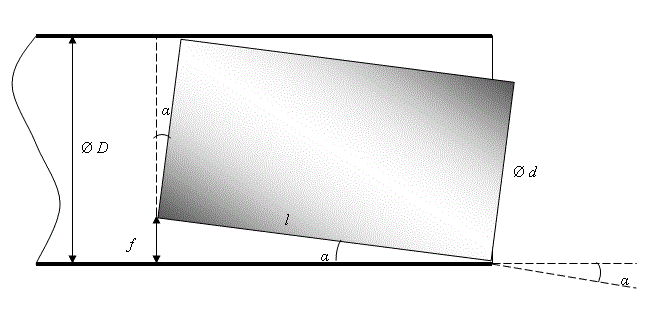
Поскольку прогресс в гауссостроении не стоит на месте, и появляются все новые и новые модели, имеющие достаточно высокую начальную скорость метаемого тела (снаряда), то, на мой взгляд, настал момент, когда можно поднять вопрос о точности стрельбы из койлгана. Для его рассмотрения надо сразу отметить один важный факт: дело в том, что, в отличие от огнестрельного и пневматического оружия, снаряд в электромагнитном ускорителе рассматриваемого типа движется в стволе с определенным зазором (т.е. диаметр снаряда меньше диаметра ствола). Основная причина такого положения вещей – стремление избежать любого трения, которое снижает и без того невысокий КПД ускорения койлгана. Обозначим значение зазора как δ, а его отношение к диаметру снаряда d как ∆ и посмотрим, как эти величины влияет на точность стрельбы. Для начала рассмотрим цилиндрический снаряд длиной l (см. рис. 1).
Рис. 1.
Из рисунка видно, что зазор между задним торцом снаряда, имеющего на выходе из ствола максимальный угол рассеяния α, равен:
f = l ·sin α = D - d ·cos α (1)
Отсюда, имея в виду малость α (т.е. cos α ≈1), легко получить, что
α = arcsin (δ/l)= arcsin {∆(d/l)} (2)
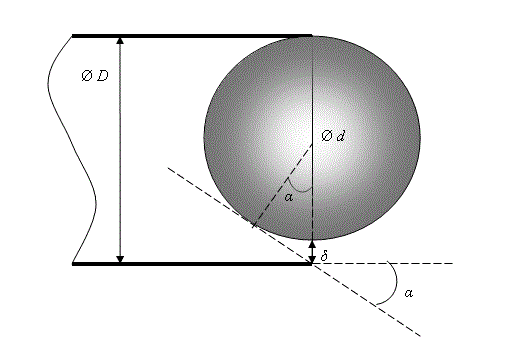
Рассмотрим теперь такую же ситуацию для шарообразного снаряда:
Рис. 2.
Здесь траектория максимального отклонения будет соответствовать касательной к поверхности снаряда, проходящей через передний срез ствола, и угол рассеивания равен:
α = arccos {d/(d+2δ)}= arccos {1/(1+2∆)} (3)
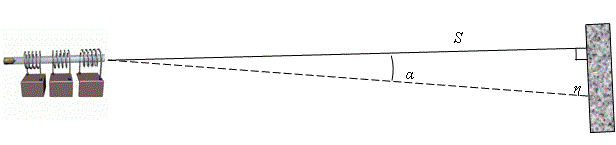
Теперь посмотрим, как рассеивание снарядов η при стрельбе на дистанцию S выражается через угол рассеивания (рис. 3):
Рис. 3.
Как видно,
η = S∙tg(α) (4)
Подставляя в (4) выражения для α, определяемые формулами (2) и (3), получим по известным тригонометрическим соотношениям с учетом малости зазора (∆<<1): - для цилиндрического снаряда:
или
- для шарообразного снаряда:
или
Как видно, в первом случае рассеивание пропорционально ∆, а во втором – корню квадратному из ∆. Поскольку ∆<<1, то уже очевидно, что рассеивание для шарообразного снаряда намного больше. Попробуем провести численные оценки. Допустим, мы имеем калибр снаряда 8 мм и зазор 50 мкм (в реальности в любительских койлганах зазор составляет 100 мкм и более по многим причинам, главная из которых - малая жесткость и неровность тонкостенных трубок, из которых изготавливаются стволы). Тогда ∆ = 0,00625 и при стрельбе на 10 м мы получим для шарика максимальное рассеивание около 1,58 м! В этих же условиях для цилиндрического снаряда с соотношением диаметра и длины 1/3 рассеивание составит только 2,1 см. Естественно, эти цифры отражают лишь качественную зависимость, поскольку снаряды вовсе не обязаны всегда лететь по обозначенной на рисунках выше траектории максимального отклонения, однако тенденция очевидна - рассеивание для цилиндрических снарядов намного меньше, чем для шарообразных. Интуитивно это объяснимо, поскольку продолговатый цилиндрический корпус играет роль своеобразного "стабилизатора", не давая телу сильно отклоняться от траектории на выходе из ствола. Интересно сравнить эти умозрительные оценки с результатами реальных экспериментов по исследованию точности стрельбы из койлгана ЕМ-3, которые я приводил здесь. В данном случае имеем цилиндрический снаряд калибром 5,5 мм и отношением d/l около 0,035, движущийся в стволе с внутренним диаметром 5,9 мм. По формуле (5) получаем для дистанции 10 м рассеивание 2,56 см, что прекрасно подтверждается результатом эксперимента (радиус отклонения при повторной стрельбе одной стрелой около 2,5 см) . Такое точное совпадение, конечно, случайно, поскольку мы не учитывали множество факторов (например, гибкость стабилизатора снаряда в данном конкретном случае), но оно иллюстрирует правильность предложенного подхода.
| |
| Просмотров: 696 | |
| Всего комментариев: 0 | |
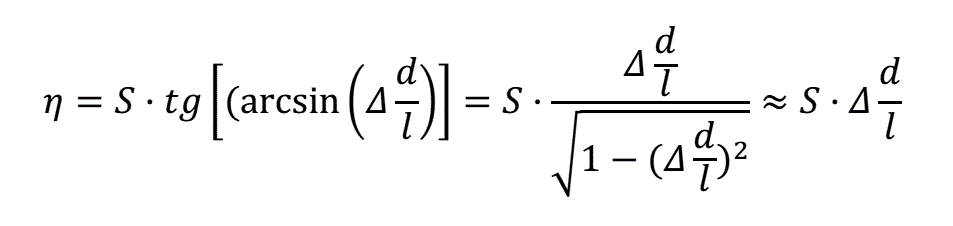 (5)
(5)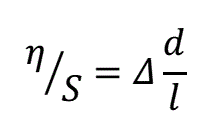 (5a)
(5a)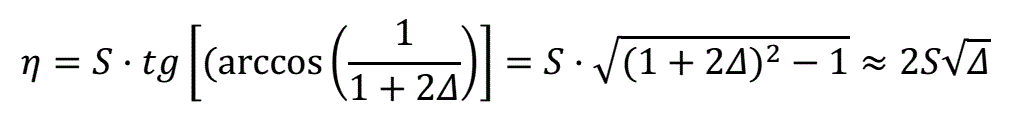 (6)
(6)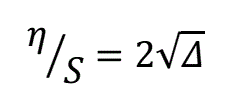 (6а)
(6а)